| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 데이터베이스
- 다이나믹 프로그래밍
- 자바스크립트
- Python
- 브루트포스 알고리즘
- 너비우선탐색
- 브루트포스
- DFS
- 백트래킹
- BFS
- 프로그래머스
- 너비 우선 탐색
- 백준알고리즘
- SWEA
- 백준 알고리즘
- 다익스트라
- 그래프 이론
- SW Expert Academy
- javascript
- oracle
- 그리디 알고리즘
- 문자열
- 그래프 탐색
- 이분 탐색
- 오라클
- 완전탐색
- DP
- 스택
- 파이썬
- 구현
- Today
- Total
민규의 흔적
[Python 파이썬] 프로그래머스 - 섬 연결하기 본문
2024년 6월 18일
문제 링크 : 프로그래머스 - 섬 연결하기
문제 접근
모든 섬을 최소 비용으로 연결했을 때, 해당 비용을 출력하는 문제이다.
이어져있지 않은 섬은 존재하지 않기에, 최소 신장 트리(MST)를 찾는 문제라고 판단해 크루스칼 알고리즘을 활용하고자 하였다.
다음과 같은 그래프가 있다고 가정해보겠다.
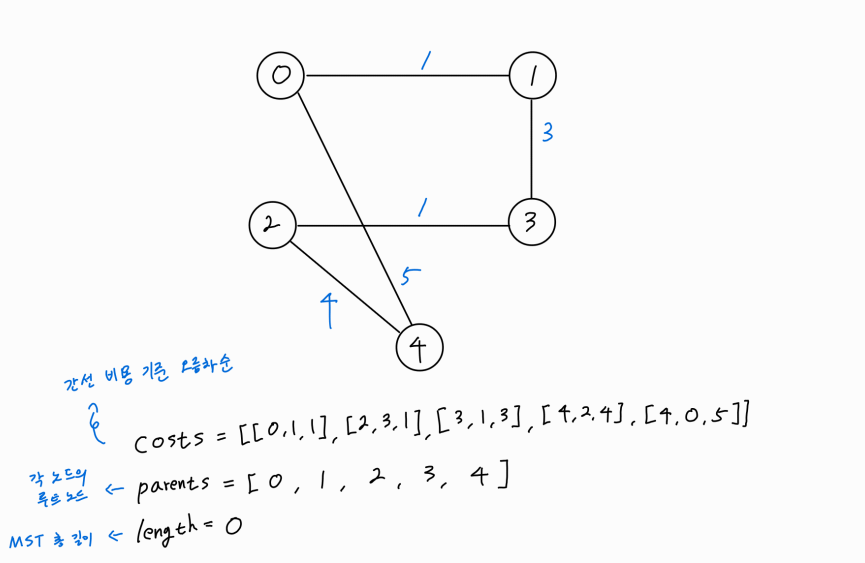
모든 간선의 정보를 비용을 기준으로 오름차순 정렬하고, 각 노드의 루트 노드 정보를 담을 배열을 선언 및 초기화, MST의 총 길이를 나타내는 length를 선언한다.
두 노드 중 어느 노드를 부모 노드로 할 지 통일시켜주기 위해, 번호가 더 작은 노드를 부모노드로 지정하는 것으로 통일시켜주겠다.
이제부터, 각 간선의 정보를 앞에서부터 확인하며 탐색을 진행해보자.

0번 노드와 1번 노드의 루트 노드가 다르므로, 둘을 연결시켜도 사이클이 형성되지 않는다.
두 노드를 잇는 간선을 MST 구성 간선으로 채택하고 번호가 더 큰 1번 노드의 루트 노드를 0번 노드의 루트 노드 번호로 변경시켜준 뒤, length를 1 증가시켜준다.

2번 노드와 3번 노드의 루트 노드가 다르므로, 둘을 연결시켜도 사이클이 형성되지 않는다.
두 노드를 잇는 간선을 MST 구성 간선으로 채택하고 번호가 더 큰 3번 노드의 루트 노드를 2번 노드의 루트 노드 번호로 변경시켜준 뒤, length를 1 증가시켜준다.

3번 노드와 1번 노드의 루트 노드가 다르므로, 둘을 연결시켜도 사이클이 형성되지 않는다.
두 노드를 잇는 간선을 MST 구성 간선으로 채택하고 번호가 더 큰 3번 노드의 루트 노드를 1번 노드의 루트 노드 번호로 변경시켜준 뒤, length를 3 증가시켜준다.
해당 과정에서, 3번 노드와 연결되어 있는 2번 노드 또한 루트 노드가 1번 노드의 루트 노드 번호로 갱신시켜 각 노드가 서로 연결되었음을 암시해준다.

4번 노드와 2번 노드의 루트 노드가 다르므로, 둘을 연결시켜도 사이클이 형성되지 않는다.
두 노드를 잇는 간선을 MST 구성 간선으로 채택하고 번호가 더 큰 4번 노드의 루트 노드를 2번 노드의 루트 노드 번호로 변경시켜준 뒤, length를 4 증가시켜준다.

4번 노드와 0번 노드의 루트 노드가 같기 때문에, 둘을 연결시키면 사이클이 생기게 된다.
MST에서 사이클은 존재하면 안되므로 해당 간선은 MST 구성 간선으로 채택하지 않는다.

모든 간선을 탐색하였으므로 로직을 종료한다.
최종 MST는 위 그래프의 보라색 간선을 이은 것과 같으며, 총 간선의 길이는 9이다.
전체 코드
def find_parent(x):
global parents
# 루트노드 갱신
if parents[x] != x:
parents[x] = find_parent(parents[x])
return parents[x]
def union_parent(x, y):
global parents
x = find_parent(x)
y = find_parent(y)
if x < y:
parents[y] = x
else:
parents[x] = y
def solution(n ,costs):
global parents
answer = 0
# 비용 기준 오름차순 정렬
costs.sort(key = lambda x:x[2])
# 크루스칼로 MST찾기
# 부모 노드 저장 배열
parents = [i for i in range(n)]
for x, y, cost in costs:
if find_parent(x) != find_parent(y):
# x, y의 부모노드들 갱신
union_parent(x, y)
# x, y 노드와 연결된 모든 노드들의 부모노드 갱신
union_parent(x, y)
answer += cost
return answer
if __name__ == "__main__":
n = 5
costs = [[0, 1, 1], [2, 3, 1], [3, 1, 3], [4, 0, 5], [4, 2, 4]]
print(solution(n, costs))풀이 후기
크루스칼 알고리즘을 활용해 풀 수 있는 문제였다.
크루스칼 알고리즘은 Union-Find 알고리즘까지 활용해야 하기에, 관련 문제를 더 공부해서 내 것으로 만들어야겠다 생각했다.
'프로그래머스' 카테고리의 다른 글
| [Python 파이썬] 프로그래머스 - 의상 (0) | 2024.06.22 |
|---|---|
| [Python 파이썬] 프로그래머스 - 소수 찾기(Lv 2) (0) | 2024.06.22 |
| [Python 파이썬] 프로그래머스 - 가장 먼 노드 (0) | 2024.06.18 |
| [Python 파이썬] 백준 11723번 - 집합 (0) | 2024.06.11 |
| [Python 파이썬] 프로그래머스 - 구명보트 (0) | 2024.06.11 |

