| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 그래프 이론
- 완전탐색
- 다익스트라
- 그래프 탐색
- 문자열
- 백트래킹
- 백준 알고리즘
- oracle
- javascript
- SW Expert Academy
- 다이나믹 프로그래밍
- 구현
- 스택
- Python
- 그리디 알고리즘
- 이분 탐색
- 브루트포스
- 너비우선탐색
- BFS
- 프로그래머스
- 데이터베이스
- 너비 우선 탐색
- SWEA
- 파이썬
- DP
- DFS
- 백준알고리즘
- 오라클
- 자바스크립트
- 브루트포스 알고리즘
- Today
- Total
민규의 흔적
[Python 파이썬] 백준 15649번 - N과 M (1) 본문
2024년 6월 30일
문제 링크 : 백준 15649번 - N과 M (1)
문제
자연수 N과 M이 주어졌을 때, 아래 조건을 만족하는 길이가 M인 수열을 모두 구하는 프로그램을 작성하시오.
- 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열
입력
첫째 줄에 자연수 N과 M이 주어진다. (1 ≤ M ≤ N ≤ 8)
출력
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다.
수열은 사전 순으로 증가하는 순서로 출력해야 한다.
알고리즘 분류
- 백트래킹
문제 접근
자연수 N이 주어졌을 때, 1 ~ N 까지의 자연수 중, 중복 없이 길이 M만큼의 수열로 올 수 있는 모든 경우의 수를 사전 순으로 출력해야 하는 문제이다.
모든 경우의 수를 완전탐색 해야하는 문제이므로 백트래킹 기법을 사용해야겠다 라고 생각했다.
백트래킹을 활용한 동작 과정에 대한 이해는 크게 어렵지 않다.
우리가 만약 1, 2, 3, 4의 숫자 카드 하나씩 가지고, 네 자리 숫자를 만드는 모든 경우의 수를 찾아본다고 가정해보자.
모두가 그런 것은 아니겠지만, 대부분 이런 방식으로 모든 경우를 찾을 것이다.
1. 일단 차례대로 나열해보자 -> [ 1 2 3 4 ]
2. 그 다음, 4를 빼고(현재 [ 1, 2, 3 ]) 마지막 숫자인 3 뒤에는 4밖에 못오는데 이미 [ 1 2 3 4 ]의 경우는 찾았으니 3도 빼놓자.
3. [ 1 2 ] 에서 3번째 자리 수에 4를 넣는 경우를 찾아보자. 그럼 그 뒤에는 3이 올 수 있네 -> 1 2 4 3
4. 앞 두 자리가 [ 1 2 ] 인 경우의 수는 다 찾았으니, 두 번째 자리까지 쭉 빼놓자 ( 현재 [ 1 ] )
5. 이제 두 번째 자리에 3을 넣어보자( 현재 [ 1 3 ]). 그럼 뒤에 올 수 있는 숫자는 2, 4인데 작은 수인 2부터 세 번째 자리에 넣어봐야겠다. (현재 [ 1 3 2 ]) 그리고 남은 수인 4를 마지막으로 넣어봐야지 -> 1 3 2 4
6. 이제 세 번째 자리 수까지 다 빼놓고(현재 [ 1 3 ]) 세 번째 자리에 4를 넣어봐야지.(현재 [ 1 3 4 ]) 그리고 남은 수인 2를 마지막으로 넣어보자. -> 1 3 4 2
7. 앞 두 자리가 [ 1 3 ] 인 경우는 다 찾았으니, 두 번째 자리까지 쭉 빼놓자 ( 현재 [ 1 ])
8. 두 번째 자리로 한 번도 못온 숫자인 4를 넣어보고(현재 [ 1 4 ]), 세 번째 자리에 올 수 있는 2, 3 중에 작은 수인 2를 먼저 넣어보자(현재 [1 4 2]). 그리고 마지막 수에 남은 숫자 3을 넣자 -> 1 4 2 3
9. 세 번째 자리 숫자까지 다 빼고(현재 [ 1 4 ]), 세 번째 숫자에 3을 넣어보자( 현재 [ 1 4 3 ]). 그리고 마지막 남은 수인 2를 넣어보자 -> 1 4 3 2
10. 첫 번째 자리가 1이고, 두 번째 자리에 2, 3, 4를 모두 넣어봤으니, 이제 맨 앞자리에 2를 넣어보고 경우의 수를 모두 구해봐야겠다.
11. 1 ~ 10 과정과 같은 방법으로 앞 자리가 4의 모든 경우까지 판단한다.
1 ~ 10 순서대로 도출한 경우의 수는 다음과 같은 순서로 나타난다.
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
오름차 순서대로 경우의 수를 찾았다. 이게 가능한 이유는, 각 자리에 올 수 있는 수가 여러 개 일때, 작은 수가 먼저 들어갈 수 있도록 고려했기 때문.
이와 같은 흐름을 그림으로 표현하면 다음과 같다.

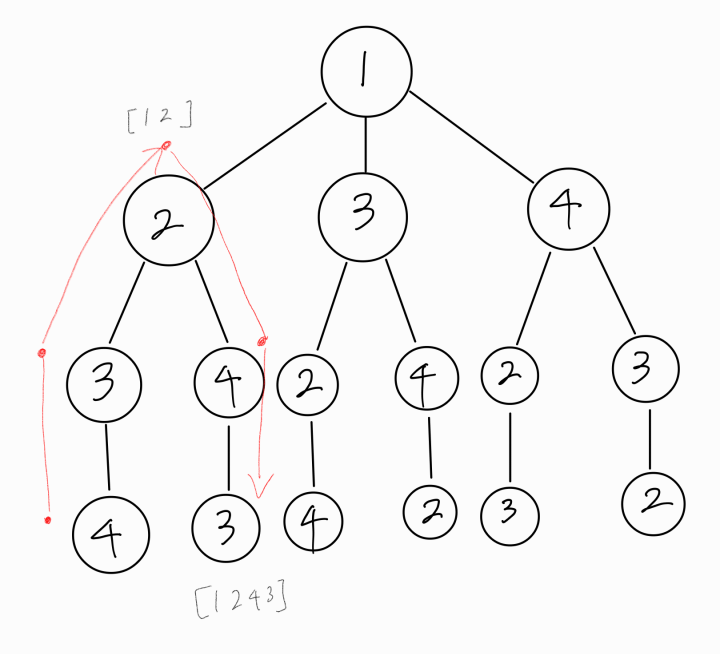




루트 노드가 2일 때 또한 고려하는 과정은 10번 과정을 뜻하며, 루트 노드를 다음 수로 옮겨가며 탐색하는 과정은 11번 과정을 의미한다.
재귀적으로 호출하며 값을 넣고, 다시 이전 상태로 돌아가는(빼는 과정) 수행하는 일련의 과정을 백트래킹 기법이라고 한다.
입력 예제
4 4
출력 예제
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
3 1 2 4
3 1 4 2
3 2 1 4
3 2 4 1
3 4 1 2
3 4 2 1
4 1 2 3
4 1 3 2
4 2 1 3
4 2 3 1
4 3 1 2
4 3 2 1
전체 코드
# 15649
def back_tracking(arr, now_length, used_num):
if now_length == M:
print(*arr)
return
for idx in range(1, N + 1):
if not used_num[idx]:
arr.append(idx)
used_num[idx]= True
back_tracking(arr, now_length + 1, used_num)
arr.pop()
used_num[idx] = False
if __name__ == "__main__":
N, M = map(int, input().split())
# 0번째 인덱스는 더미 인덱스
nums = [i + 1 for i in range(N + 1)]
used_num = [False] * (N + 1)
back_tracking([], 0, used_num)
백트래킹 기법은 재귀호출 될 함수에 어떤 인자값을 넣어줘야 하는지, 어떤 흐름으로 진행되는지 이해하는 것이 가장 중요하다.
위 함수에서는 현재 완성된 조합의 배열, 현재 조합의 길이, 사용된 숫자의 유무 정보를 전달한다.
풀이 후기
백트래킹 기법은 이해 후 여러 응용문제를 많이 접해보는 것이 중요하다고 생각한다.
'BOJ' 카테고리의 다른 글
| [JavaScript 자바스크립트], [Python 파이썬] 백준 1213번 - 팰린드롬 만들기 (1) | 2024.07.01 |
|---|---|
| [JavaScript 자바스크립트] 백준 1515번 - 수 이어 쓰기 (1) | 2024.07.01 |
| [Python 파이썬] 백준 2231번 - 분해합 (0) | 2024.06.26 |
| [Python 파이썬] 백준 2798번 - 블랙잭 (0) | 2024.06.26 |
| [Python 파이썬] 백준 1436번 - 영화감독 숌 (0) | 2024.06.26 |



