[자료구조] 힙(Heap)과 우선순위 큐(Priority Queue) [ 프로그래머스

Notice

Recent Posts

Recent Comments

Link

« 2025/01 »
일	월	화	수	목	금	토
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

Tags more

Archives

Today

Total

관리 메뉴

민규의 흔적

[자료구조] 힙(Heap)과 우선순위 큐(Priority Queue) [ 프로그래머스 - 더 맵게 ] by JavaScript 본문

자료구조

[자료구조] 힙(Heap)과 우선순위 큐(Priority Queue) [ 프로그래머스 - 더 맵게 ] by JavaScript

민규링 2024. 7. 7. 02:38

2024년 7월 7일

힙(Heap)

힙이란, 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리 기반의 자료구조이다.
부모 노드와 자식 노드의 일련된 대소 관계가 성립하는 구조를 보인다.

최대 힙(max heap)

부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리를 의미한다.

위 그림과 같이, 자식 노드를 가지고 있는 모든 부모 노드는 무조건 자식 노드보다 크거나 같은 값을 지니는 양상을 보인다.

최소 힙(min heap)

부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리를 의미한다.

위 그림과 같이, 자식 노드를 가지고 있는 모든 부모 노드는 무조건 자식 노드보다 크거나 같은 값을 지니는 양상을 보인다.

부모 노드와 자식 노드의 연결 관계

부모 노드와 자식 노드의 연결관계는 위 그림과 같이 부모 노드 인덱스 * 2, 부모 노드 인덱스 * 2 + 1로 접근 가능하다.

최대 힙의 삽입 연산

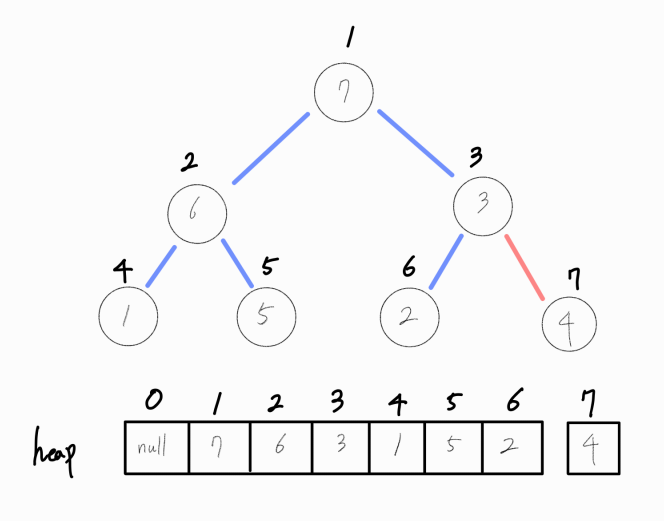
기존 최대 힙에 4라는 값을 삽입했다고 가정해보자.

일단, 배열의 맨 끝에 해당 값을 추가해준다.
이는 완전 이진트리 형태의 그림으로 표현한다면 위 그림과 같이 완전 이진트리에서 마지막으로 올 수 있는 리프노드의 위치이다.

위 트리는 최대 힙 구조를 보이는가? 아니다!
최대 힙 구조라면 전체적인 구조면에서 부모 노드는 무조건 자식 노드보다 커야하는데, 삽입된 노드의 부모 노드가 더 작기 때문이다.
삽입한 이후 다시 최대 힙 구조로 재정립하는 연산 과정을 거쳐야 한다.

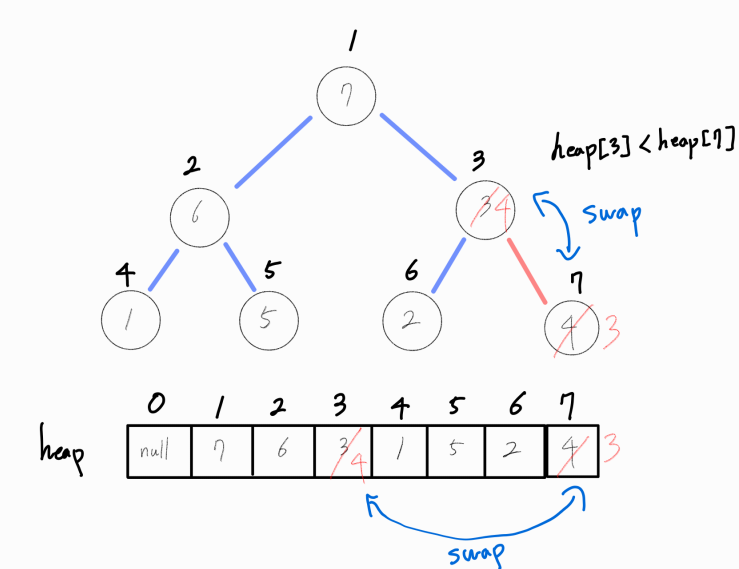
현재 삽입된 노드와 부모 노드를 비교해, 부모 노드가 더 작다면 계속 둘의 값을 바꿔주어야 한다.

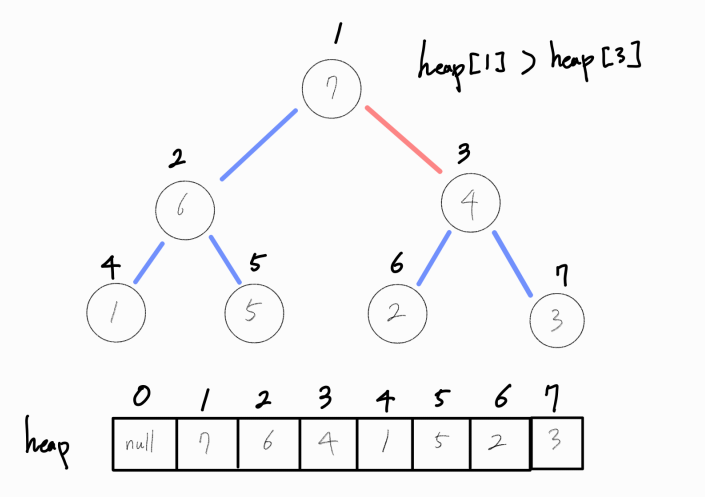
연산을 진행하며 부모 노드와 비교해, 부모 노드가 더 크다면 연산을 종료한다.

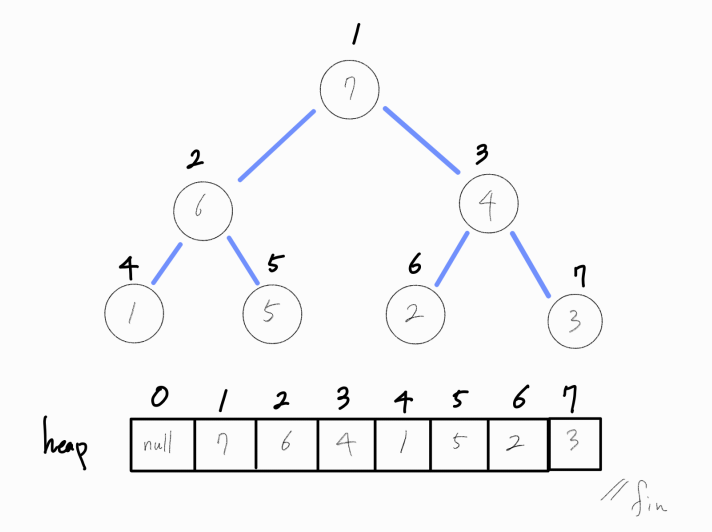
최대 힙의 삭제 연산

최대 힙 구조는 최대값을 빠르게 추출해낼 수 있다는 특징이 있다.

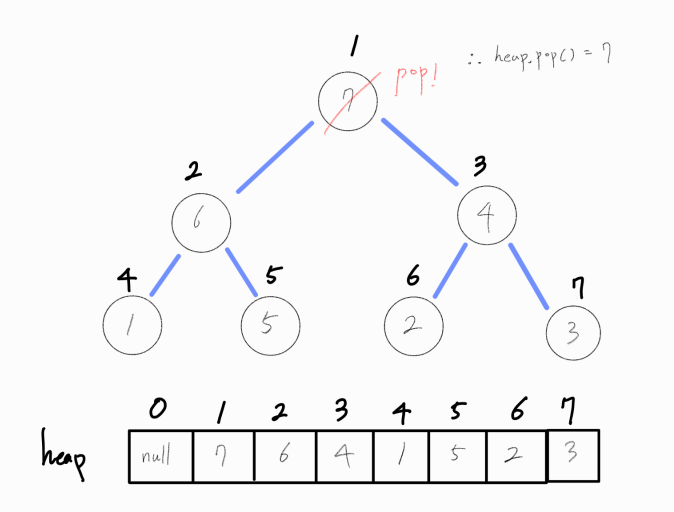
최대 힙 구조에서 최대값은 루트노드이며, 이는 heap[1]이다. 이 값을 pop하여 뽑아내면 루트 노드가 비게 된다.
루트 노드가 비었으므로 루트 노드에 최대값을 지닌 노드가 오도록 연산을 추가로 진행해야 한다.

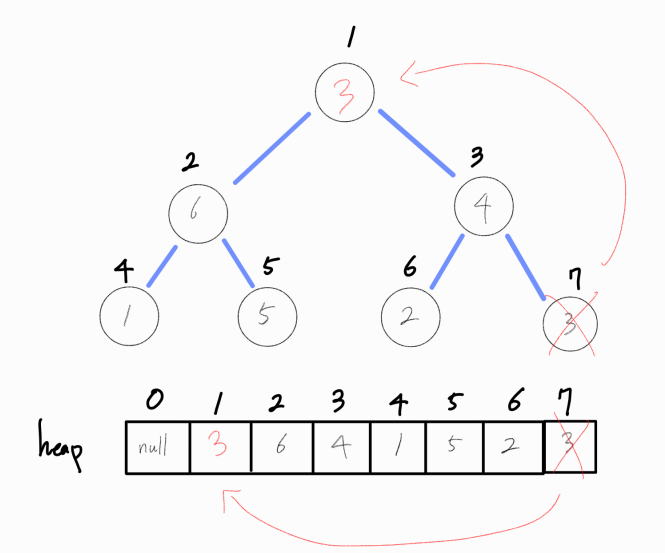
루트 노드를 추출해냈다면, 루트 노드를 heap의 마지막 노드로 채워둔다.

그리고 최대 힙 구조를 만족하기 위해 추가 연산을 진행한다.

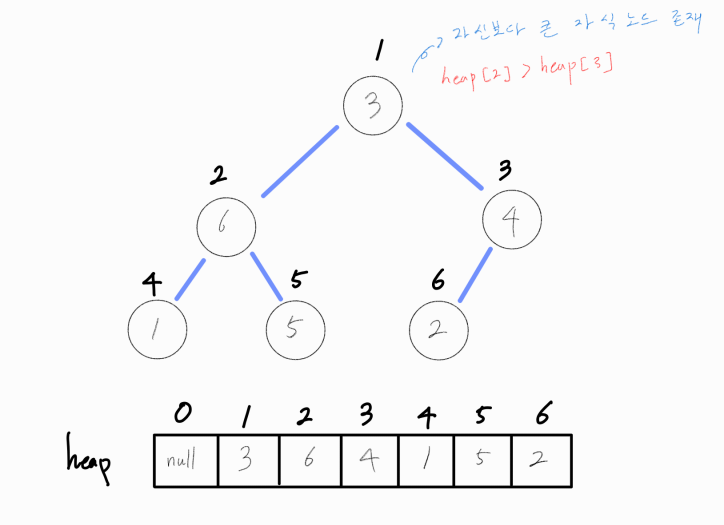
루트 노드를 기준으로, 자식 노드에 더 큰 값이 존재한다면 둘을 바꿔준다.

만약 자식 노드가 모두 현재 노드보다 크다면 더 큰 자식 노드 값과 바꿔준다. 루트 노드는 최대값이어야 하기 때문에 더 큰 값이 오도록 유도해야 하기 때문이다.

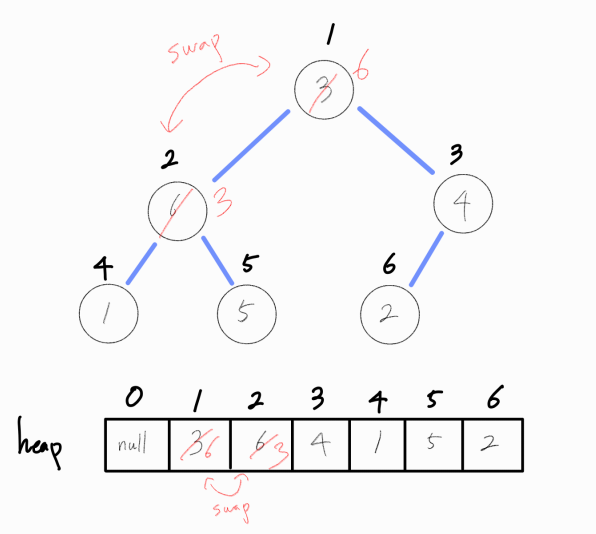
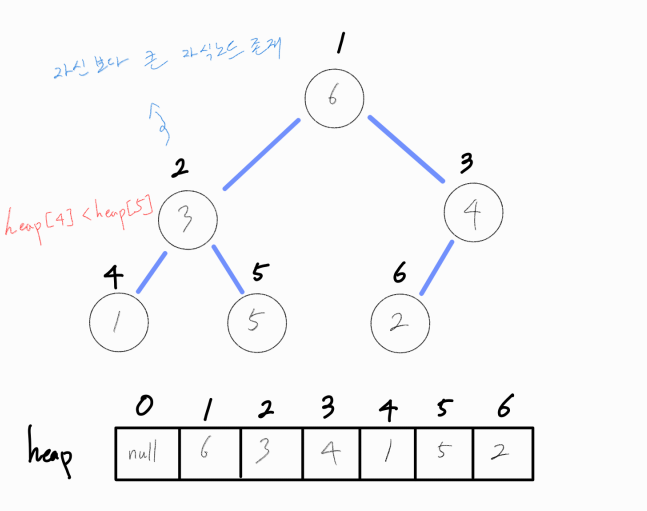
두 노드를 swap 하였지만, 아직 현재 노드의 자식 노드가 더 큰 양상을 보인다.

최대 힙 조건을 아직 만족하지 않으므로 더 큰 자식노드와 현재 노드를 swap 해준다.

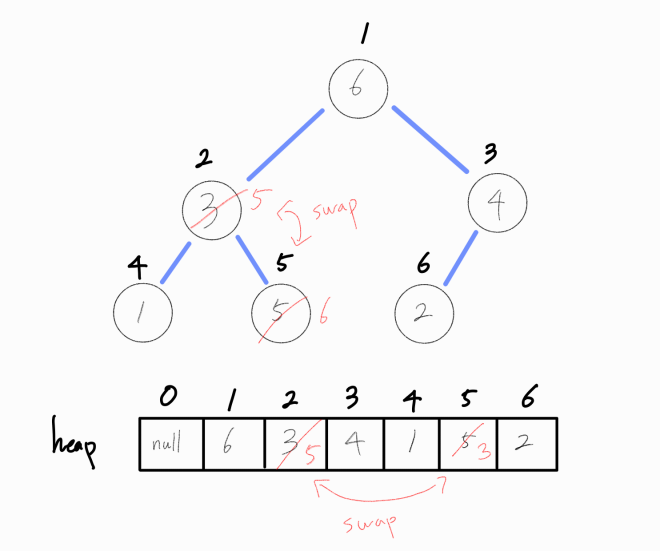
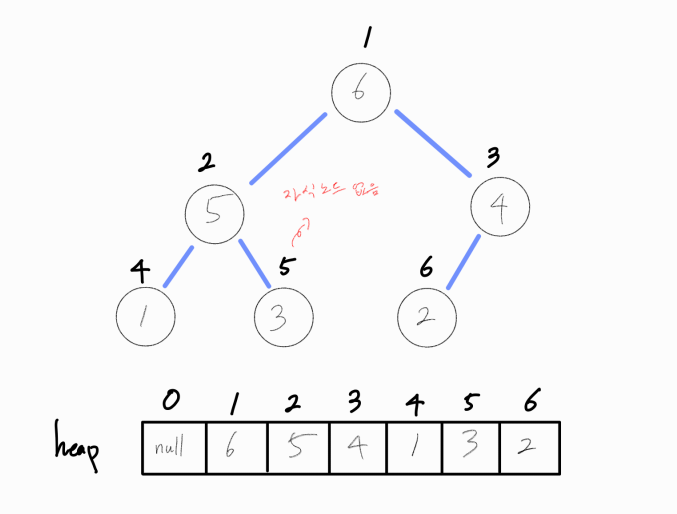
더 이상 자식 노드가 존재하지 않기에(리프 노드) 연산을 종료한다.

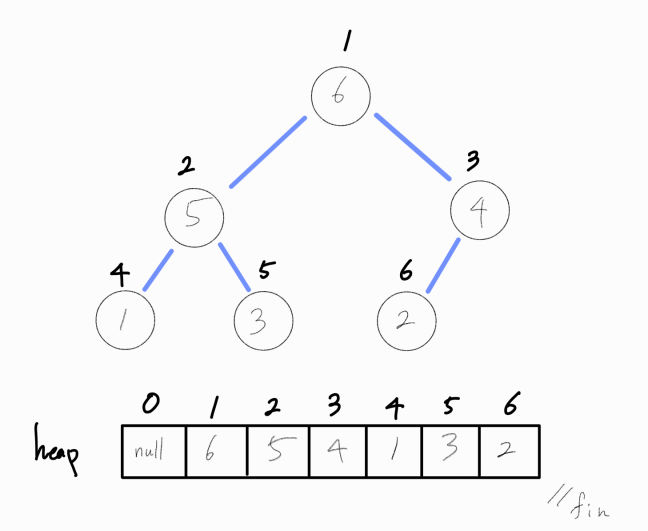
최소 힙의 삽입 연산

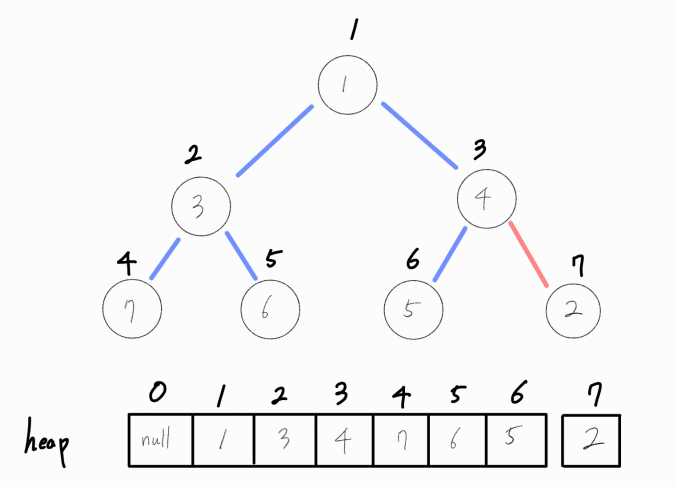
기존 최소 힙에 2 라는 값을 삽입한다고 가정해보자.

일단, 배열의 맨 끝에 해당 값을 추가해준다.
이는 완전 이진트리 형태의 그림으로 표현한다면 위 그림과 같이 완전 이진트리에서 마지막으로 올 수 있는 리프노드의 위치이다.

위 트리는 최소 힙 구조를 보이는가? 아니다!
최소 힙 구조라면 전체적인 구조면에서 부모 노드는 무조건 자식 노드보다 작아야하는데, 삽입된 노드의 부모 노드가 더 크기 때문이다.
삽입한 이후 다시 최소 힙 구조로 재정립하는 연산 과정을 거쳐야 한다.

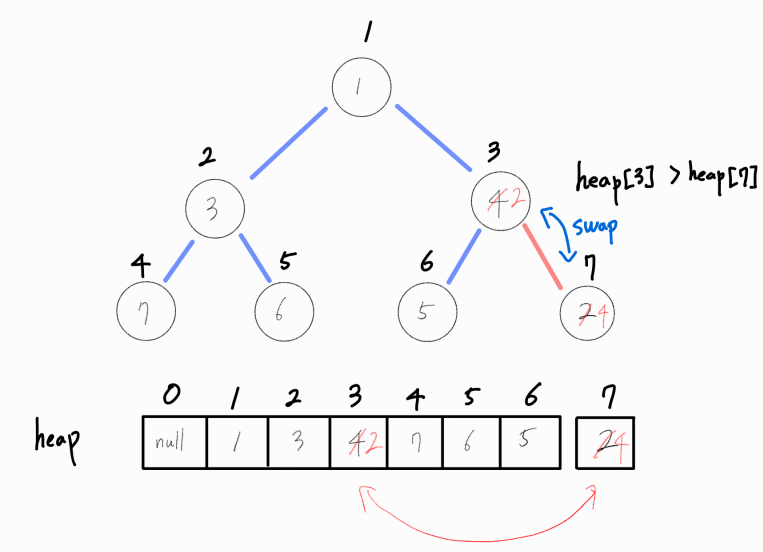
현재 삽입된 노드와 부모 노드를 비교해, 부모 노드가 더 크다면 계속 둘의 값을 바꿔주어야 한다.

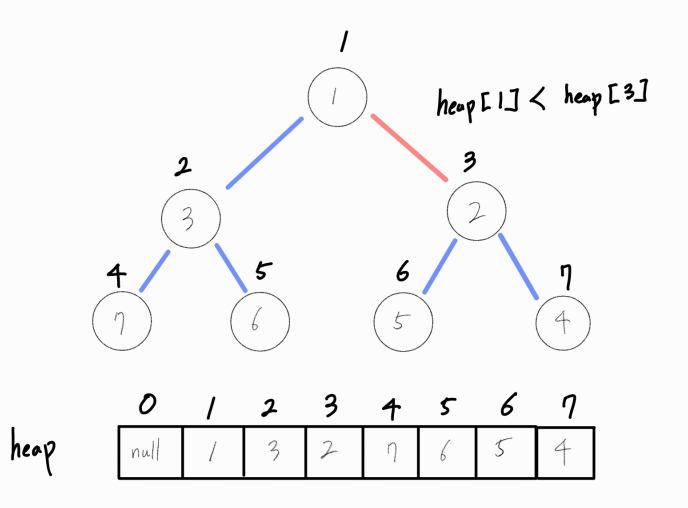
부모 노드와 비교해, 부모 노드가 더 작다면 연산을 종료한다.

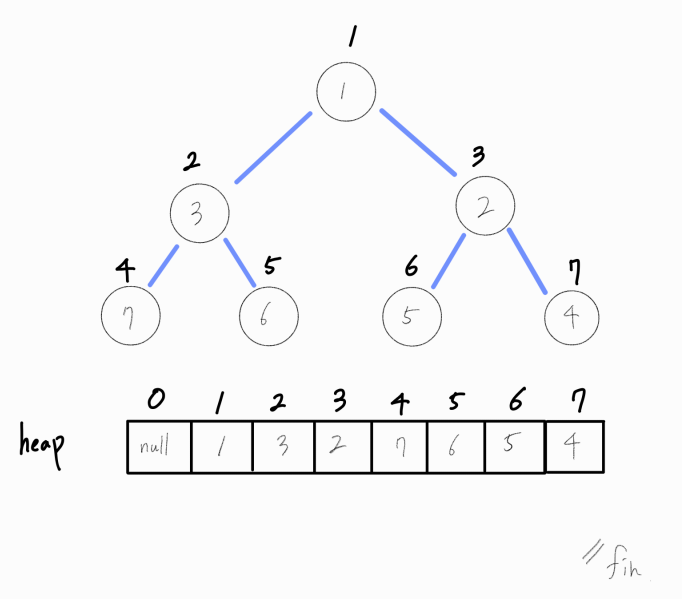
최소 힙의 삭제 연산

최소 힙 구조는 최소값을 빠르게 추출해낼 수 있다는 특징이 있다.

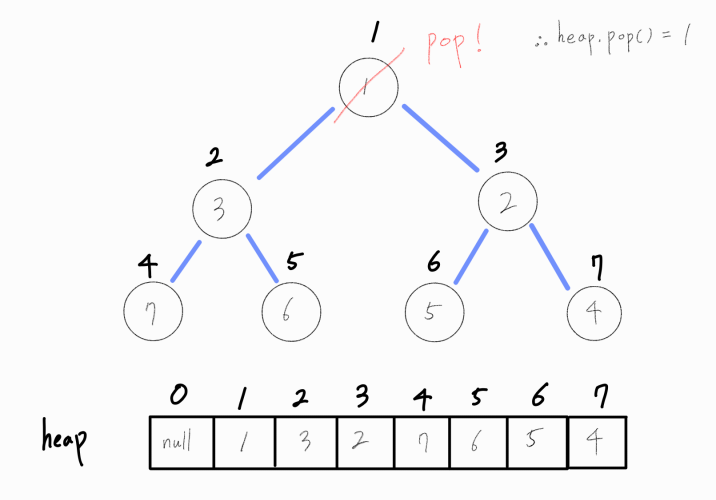
최소 힙 구조에서 최소값은 루트노드이며, 이는 heap[1]이다. 이 값을 pop하여 뽑아내면 루트 노드가 비게 된다.
루트 노드가 비었으므로 루트 노드에 최소값을 지닌 노드가 오도록 연산을 추가로 진행해야 한다.

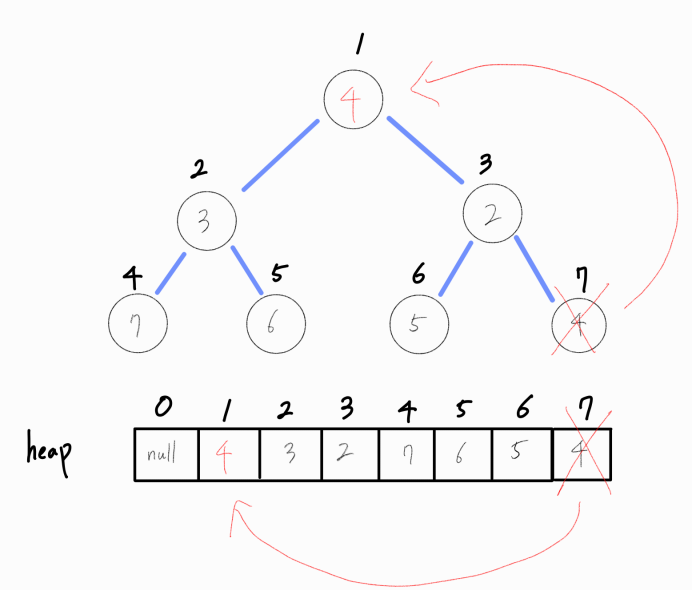
루트 노드를 추출해냈다면, 루트 노드를 heap의 마지막 노드로 채워둔다.

그리고 최소 힙 구조를 만족하기 위해 추가 연산을 진행한다.

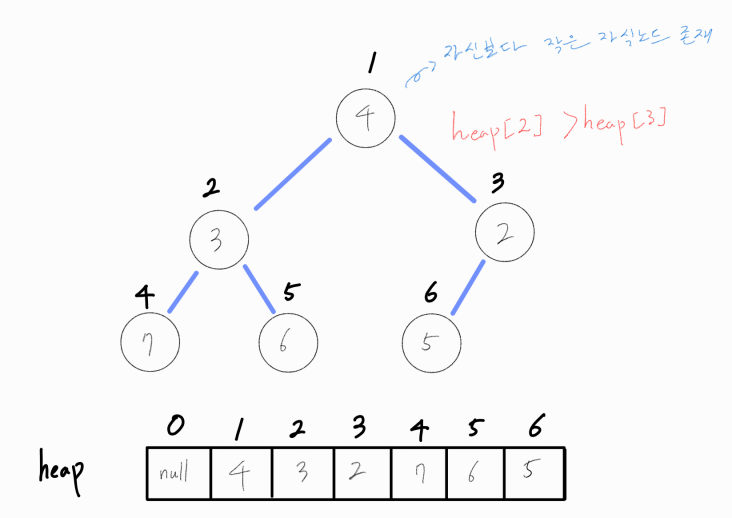
루트 노드를 기준으로, 자식 노드에 더 작은 값이 존재한다면 둘을 바꿔준다.

만약 자식 노드가 모두 현재 노드보다 작다면 더 작은 자식 노드 값과 바꿔준다. 루트 노드는 최소값이어야 하기 때문에 더 작은 값이 오도록 유도해야 하기 때문이다.

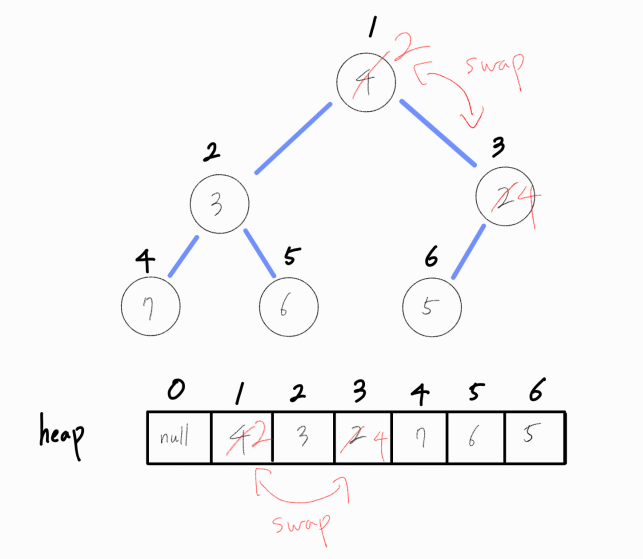
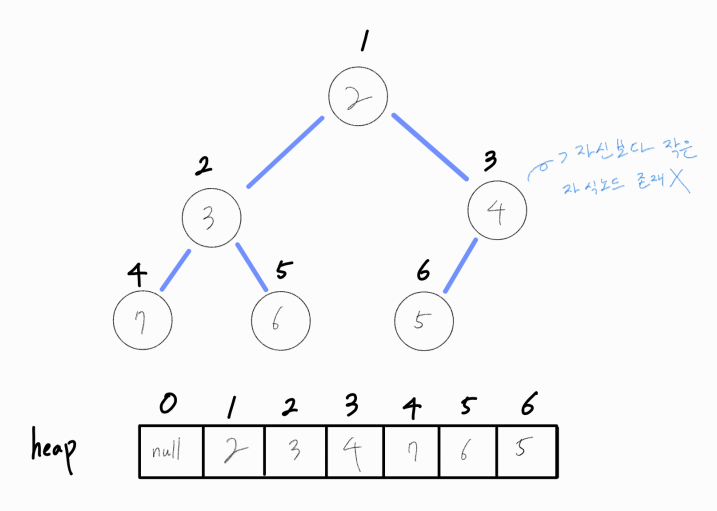
더 이상 자식 노드가 현재 노드보다 작지 않으니, 연산을 종료한다.

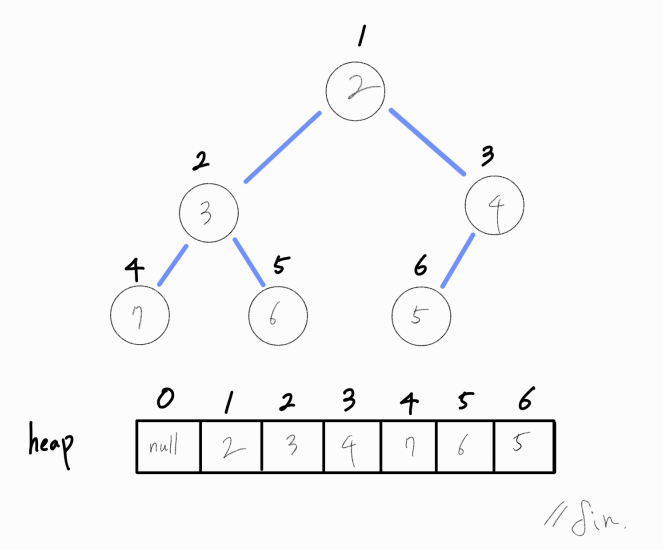
최소 힙과 최대 힙의 구현 차이

최소 힙은 노드가 root에 가까워 질 수록 점점 작아지며 root 노드는 최솟값을 지니고 있다.
반대로 최대 힙에서는 root 노드는 최댓값을 지니고 있다.

여기서 말하고 싶은 것은, 최소 힙과 최대 힙 구현 로직은 따로 작성할 필요가 없다.

만약 내가 최소 힙 구조를 구현할 줄 아는데 최대 힙 구조를 구현하고 싶다면, 추가로 로직을 구현할 필요 없이 모든 데이터에 -1을 곱해주면 되기 때문이다.

최소 힙의 최솟값을 추출하고, 해당 값에 -1을 곱하면 결국 최댓값을 얻어낼 수 있다.

우선순위 큐(Priority Queue)

큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First In First Out) 형태의 자료구조이다.
우선순위 큐(Priority Queue)는 먼저 들어오는 데이터가 아닌, 우선순위가 높은 데이터가 먼저 나가는 형태의 자료구조이다.

힙 얘기하다 말고 우선순위 큐를 왜 얘기하느냐? 우선순위 큐를 일반적으로 힙을 이용해 구현하기 때문이다.

숫자가 낮을 수록 우선순위가 높다고 가정한다면, 최소 힙 구조를 이용해 우선순위가 가장 높은 데이터를 루트로 지정해 빠르게 데이터를 뽑고, 삭제 연산을 통해 다음 우선순위의 데이터를 루트에 위치하도록 할 것이다.
또한 새로운 데이터가 들어왔을 때 해당 데이터의 우선순위가 어떻게 되는지에 따라 삽입 연산을 통해 적절한 곳에 데이터가 위치하도록 할 수 있을 것이다.

숫자가 높을 수록 우선순위가 높다고 가정한다면, 최대 힙 구조를 이용해 위와 같이 구성할 수 있을 것이다.

이와 같이 새로운 데이터가 주기적으로 삽입되거나 기존의 데이터가 삭제될 때마다 변동되는 우선순위를 빠르게 정립하기 위해 힙 구조를 활용한다.

이는 다음의 시간복잡도에서 추가로 후설하겠다.

시간 복잡도

로직	시간복잡도
최소(최대)값 찾기	O(1)
삽입 연산	O(lg N)
삭제 연산	O(lg N)

최소(최대)값은 루트 노드를 참조하면 되므로 시간복잡도가 O(1)이다.

어떤 값을 삽입하거나 삭제하였을 때, 다시 힙 구조로 재정립하는 시간복잡도는 O(lg N)이다. 이는 부모 < - > 자식을 비교해보며 둘을 swap하는 과정을 통해 이루어지므로 힙의 높이만큼 연산을 진행하게 된다. 노드의 개수가 N개일 때 힙의 높이는 lg N 이므로 시간복잡도는 O(lg N)이 된다.

이는 주기적으로 새로운 데이터가 추가되거나 최소(최대)값을 추출해낼 때 힙 구조가 유용한 이유이다.

배열이나 연결리스트의 경우 최소(최대)값을 찾으려면 모든 요소를 순회해야 하므로 O(N) 만큼의 시간복잡도를 가지고, 주기적으로 새로운 데이터가 추가되거나 최소(최대)값을 추출해내게 되면 또 O(N) 만큼의 시간복잡도를 가지므로 효율적이지 못할 수 있다.

하지만, 힙 구조를 활용한다면 O(lg N)까지 단축시킬 수 있으므로 경우에 따라 아주 효율적인 시간복잡도를 노릴 수 있게 된다.

파이썬의 heapq, 자바의 PriorityQueue, C++의 queue 등 각 언어에서 지원하는 라이브러리를 불러와 쉽게 힙 구조를 사용할 수 있다. 하지만 자바스크립트의 경우 라이브러리가 없기 때문에 힙을 직접 구현해야 한다.
(참고 : 파이썬 heapq 라이브러리 문서)

최소 힙 구현(by JavaScript)

/**
 * 힙 구조
 *              1
 *          2       3
 *       4     5  6    7       
 * - 왼쪽 자식 인덱스 = 부모 인덱스 * 2
 * - 오른쪽 자식 인덱스 = 부모 인덱스 * 2 + 1
 * - 부모 인덱스 = Math.floor(자식 인덱스 / 2)
 * 
 */
class MinHeap {
    constructor() {
        // 0번째 인덱스는 더미 인덱스
        this.hq = [null];
    }
    // 힙의 사이즈를 return
    size() {
        return this.hq.length - 1;
    }
    // x 노드와 y 노드를 서로 바꿈
    swap(x, y) {
        [this.hq[x], this.hq[y]] = [this.hq[y], this.hq[x]];
    }
    // 최소값을 return
    peek() {
        return this.hq[1];
    }
    /**
     * 삽입 연산 로직
     * 1. hq의 마지막 위치에 요소 추가 -> hq.push()
     * 2. 초기 위치에서부터, 부모 노드와 새로 추가된 노드의 값을 비교하며, 새로 추가된 값이 부모 노드 값보다 작다면 둘의 위치를 교환한다.
     * 3. 추가된 노드 값이 부모 노드보다 클 때까지 반복한다.
     */
    heappush(x) {
        this.hq.push(x) // 1

        let idx = this.size(); // 2 ~ 3
        let parent_idx = Math.floor(idx / 2);
        while (idx > 1 && this.hq[idx] < this.hq[parent_idx]) {
            this.swap(idx, parent_idx);
            idx = parent_idx;
            parent_idx = Math.floor(idx / 2);
        }
    }

    /**
     * 삭제 연산 로직
     * 1. hq에서 가장 작은 값인 루트 노드를 제거한다. 그리고 hq의 마지막 요소를 루트로 이동시킨다.
     * 2. 새로운 루트 노드와 자식 노드의 값을 비교하며, 자식 노드의 값이 작다면 루트 노드의 위치를 교환한다.
     * 3. 자식 노드의 값이 더 클 때까지 반복한다.
     */
    heappop() {
        // 힙의 크기가 1이라면 null과 root만 존재한다는 뜻.
        if (this.size() <= 1) {
            return this.hq.pop();
        }

        const value = this.hq[1]; // 1
        this.hq[1] = this.hq.pop();

        let idx = 1; // 2
        let left_idx = idx * 2;
        let right_idx = idx * 2 + 1;

        // 왼쪽 자식 노드가 존재하면서 값이 부모 노드보다 작거나
        // 오른쪽 자식 노드가 존재하면서 값이 부모 노드보다 작은 경우 계속 수행
        while ( // 3
            (this.hq[left_idx] && this.hq[left_idx] < this.hq[idx])
            ||
            (this.hq[right_idx] && this.hq[right_idx] < this.hq[idx])
        ) {
            // 더 작은 자식 노드와 교체
            if (this.hq[right_idx] && this.hq[right_idx] < this.hq[left_idx]) {
                this.swap(idx, right_idx);
                idx = right_idx
            }
            else {
                this.swap(idx, left_idx);
                idx = left_idx
            }
            left_idx = idx * 2;
            right_idx = idx * 2 + 1;
        }

        return value;

    }
}

최대 힙을 구현하고자 한다면 모든 데이터에 -1을 곱해 최소 힙 형태로 구현하면 된다. 최소값을 추출하여 해당 값에 -1을 다시 곱하여 최대값을 얻어낼 수 있다.

응용 문제

프로그래머스 - 더 맵게

문제 풀이

스코빌 지수가 가장 낮은 음식과 두 번째로 스코빌 지수가 낮은 음식을 적절히 섞으며 모든 음식의 스코빌 지수가 K 이상이 될 때까지 이를 반복한다.

음식을 섞고 난 이후의 스코빌 지수는 다음과 같이 나타낸다.

섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 + (두 번째로 맵지 않은 음식의 스코빌 지수 * 2)

기존 데이터들의 최소값을 2번 연속 뽑아내고, 해당 값을 연산을 통해 다시 삽입하여 우선순위가 계속 달라지는 형태를 보인다. 힙 구조를 쓰기 아주 적합한 문제이다.

모든 음식의 스코빌 지수를 기준으로 최소 힙 구조의 자료구조를 구축한다.

이후, 2번 연속 삭제 연산을 진행하여 최소값을 2번 연속 뽑아낸다.

두 스코빌 지수를 위와 같이 연산하여 도출한 새로운 음식의 스코빌 지수를 힙에 삽입한다.

삽입 연산을 통해 제 위치를 찾도록 유도하고, 위 과정을 조건에 부합할 때까지 계속 반복한다.

조건에 부합하는지 알려면 최소값이 K 이상이면 된다. 최소값이기 때문.

로직을 끝까지 수행했음에도 최소값이 K 미만이라면 -1을 출력한다.

전체 코드

class MinHeap {
    constructor() {
        // 0번째 인덱스는 더미 인덱스
        this.hq = [null];
    }

    size() {
        return this.hq.length - 1;
    }

    swap(x, y) {
        [this.hq[x], this.hq[y]] = [this.hq[y], this.hq[x]];
    }

    peek() {
        return this.hq[1];
    }
    /**
     * 삽입 연산 로직
     * 1. hq의 마지막 위치에 요소 추가 -> hq.push()
     * 2. 초기 위치에서부터, 부모 노드와 새로 추가된 노드의 값을 비교하며, 새로 추가된 값이 부모 노드 값보다 작다면 둘의 위치를 교환한다.
     * 3. 추가된 노드 값이 부모 노드보다 클 때까지 반복한다.
     */
    heappush(x) {
        this.hq.push(x) // 1

        let idx = this.size(); // 2 ~ 3
        let parent_idx = Math.floor(idx / 2);
        while (idx > 1 && this.hq[idx] < this.hq[parent_idx]) {
            this.swap(idx, parent_idx);
            idx = parent_idx;
            parent_idx = Math.floor(idx / 2);
        }
    }

    /**
     * 삭제 연산 로직
     * 1. hq에서 가장 작은 값인 루트 노드를 제거한다. 그리고 hq의 마지막 요소를 루트로 이동시킨다.
     * 2. 새로운 루트 노드와 자식 노드의 값을 비교하며, 자식 노드의 값이 작다면 루트 노드의 위치를 교환한다.
     * 3. 자식 노드의 값이 더 클 때까지 반복한다.
     */
    heappop() {
        // 힙의 크기가 1이라면 null과 root만 존재한다는 뜻.
        if (this.size() <= 1) {
            return this.hq.pop();
        }

        const value = this.hq[1]; // 1
        this.hq[1] = this.hq.pop();

        let idx = 1; // 2
        let left_idx = idx * 2;
        let right_idx = idx * 2 + 1;

        // 왼쪽 자식 노드가 존재하면서 값이 부모 노드보다 작거나
        // 오른쪽 자식 노드가 존재하면서 값이 부모 노드보다 작은 경우 계속 수행
        while ( // 3
            (this.hq[left_idx] && this.hq[left_idx] < this.hq[idx])
            ||
            (this.hq[right_idx] && this.hq[right_idx] < this.hq[idx])
        ) {
            // 더 작은 자식 노드와 교체
            if (this.hq[right_idx] && this.hq[right_idx] < this.hq[left_idx]) {
                this.swap(idx, right_idx);
                idx = right_idx
            }
            else {
                this.swap(idx, left_idx);
                idx = left_idx
            }
            left_idx = idx * 2;
            right_idx = idx * 2 + 1;
        }

        return value;

    }
}

function solution(scoville, K) {
    var answer = 0;

    const hq = new MinHeap();

    scoville.forEach((s) => {
        hq.heappush(s);
    });

    while (hq.size() >= 2 && hq.peek() < K) {
        const minimum_1 = hq.heappop();
        const minimum_2 = hq.heappop();
        hq.heappush(minimum_1 + minimum_2 * 2);
        answer += 1;

    }

    if (hq.peek() < K) {
        return -1;
    }

    return answer;
}

console.log(solution([1, 2, 3, 9, 10, 12], 7))

저작자표시 비영리 변경금지