| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 너비우선탐색
- SW Expert Academy
- Python
- javascript
- 브루트포스 알고리즘
- 너비 우선 탐색
- 그리디 알고리즘
- 다익스트라
- 백준 알고리즘
- 그래프 이론
- DP
- 문자열
- BFS
- 자바스크립트
- 백트래킹
- 프로그래머스
- 백준알고리즘
- 구현
- oracle
- 완전탐색
- 브루트포스
- 오라클
- 파이썬
- SWEA
- 다이나믹 프로그래밍
- 데이터베이스
- DFS
- 깊이우선탐색
- 스택
- 그래프 탐색
- Today
- Total
민규의 흔적
[Python 파이썬] 백준 9095번 - 1, 2, 3 더하기 본문
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.
출력
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
알고리즘 분류
- 다이나믹 프로그래밍
문제 접근
테스트 케이스마다 11 미만의 양의 정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 개수를 구하는 문제이다.
이 문제에서는 n이 최대 10이라 브루트포스 방식으로도 구할 수 있겠지만, n이 엄청 크다면 이는 절대 제한시간안에 풀 수 없는 문제가 된다.
기저조건인 피연산자 1, 2, 3 각각을 1, 2, 3의 합으로 나타내는 방법의 수는 다음과 같다.

n = 1일 때 1개, n = 2일 때 2개, n = 3일 때 4개의 방법을 가지고 있다.
n = 4일 때를 보자.

n = 4일 때 경우의 수들을 보면 규칙을 찾을 수 있다.
맨 뒤에 더하는 수가 1일 때, 2일 때, 3일 때를 기준으로 위처럼 나누어 보자.

맨 뒤에 더하는 수가 1일 때의 경우들은 위와 같다.
맨 뒤에 1을 더하는 것을 제외하고 본다면, n = 3일 때의 모든 방법들에 1을 더한 꼴과 같다는 것을 알 수 있다.
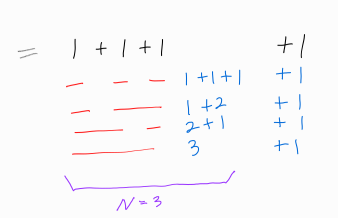
그러므로 n = 4일 때는 n = 3일 때의 모든 방법들에 1을 더한 것과 동일한 방법이 내포되어 있음을 알 수 있다.
n = 4일 때의 방법의 개수는 n = 3일때의 방법의 개수를 부분집합으로 그대로 채용해도 무방하다.
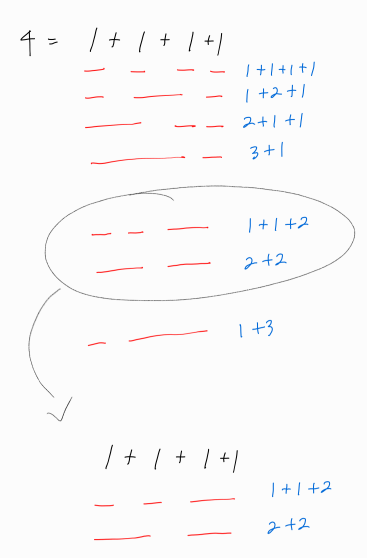
맨 뒤에 더하는 수가 2일 때의 경우들은 위와 같다.
맨 뒤에 2를 더하는 것을 제외하고 본다면, n = 2일 때의 모든 방법들에 2를 더한 꼴과 같다는 것을 알 수 있다.
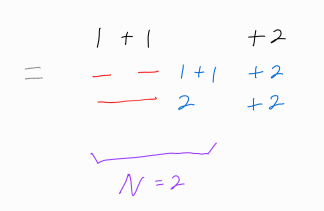
따라서 n = 4일때의 방법의 개수는 n = 2일 때의 방법의 개수를 부분집합으로 그대로 채용해도 무방하다.
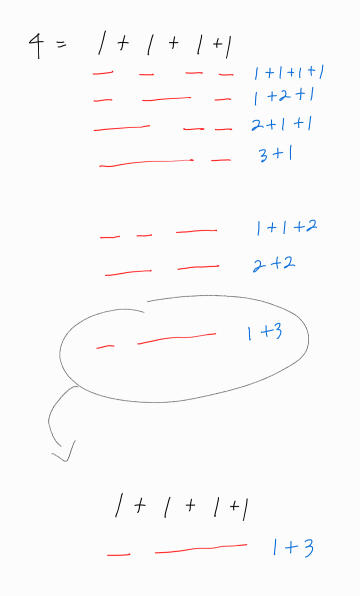
맨 뒤에 더하는 수가 3일 때의 경우는 위와 같다.
맨 뒤에 3을 더하는 것을 제외하고 본다면, n = 1일 때의 모든 방법들에 3을 더한 꼴과 같다는 것을 알 수 있다.
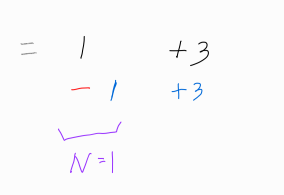
따라서 n = 4일때의 방법의 개수는 n = 1일 때의 방법의 개수를 부분집합으로 그대로 채용해도 무방하다.
여기서 우리는 점화식을 찾을 수 있는데, 이는 다음과 같다.

n이 기저조건 1 ~ 3이 아닌 4 이상의 수이며, n을 1, 2, 3의 합으로 나타내는 방법의 수는 위와 같다.
이를 말로 풀어본다면 다음과 같다.
n을 1, 2, 3의 합으로 나타내는 방법은,
● n - 1의 모든 방법의 수 각각에 1을 더하는 것
● n - 2의 모든 방법의 수 각각에 2을 더하는 것
● n - 3의 모든 방법의 수 각각에 3을 더하는 것
과 같으므로 n - 1의 방법의 가짓수, n - 2의 방법의 가짓수, n - 3의 방법의 가짓수를 모두 더한 개수가 n을 나타내는 방법의 가짓수가 된다.
입력 예제
3
4
7
10
출력 예제
7
44
274
전체 코드
# 9095
if __name__ == "__main__":
# 기저 조건 n = 1 ~ 3, 0번째 인덱스는 더미 인덱스
dp = [0, 1, 2, 4]
# n은 최대 10 이므로 n = 10까지 dp를 채워줌
for i in range(4, 11):
dp.append(dp[i - 1] + dp[i - 2] + dp[i - 3])
T = int(input())
for _ in range(T):
print(dp[int(input())])
풀이 후기
현재 집합 내에 속한 부분 집합 중, 이미 다뤘던 부분 집합을 활용해내는 방향으로 규칙을 찾아야하는 전형적인 DP 문제였다.
'BOJ' 카테고리의 다른 글
| [Python 파이썬] 백준 5972번 - 택배 배송 (1) | 2024.09.26 |
|---|---|
| [Python 파이썬] 백준 1283번 - 단축키 지정 (1) | 2024.09.05 |
| [Python 파이썬] 백준 15558번 - 점프 게임 (0) | 2024.08.14 |
| [Python 파이썬] 백준 25195번 - Yes or yes (0) | 2024.08.14 |
| [Python 파이썬] 백준 17129번 - 윌리암슨수액빨이딱따구리가 정보섬에 올라온 이유 (0) | 2024.08.14 |


