| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 다익스트라
- 백트래킹
- BFS
- oracle
- 브루트포스 알고리즘
- 그래프 탐색
- 오라클
- 백준알고리즘
- 브루트포스
- Python
- SWEA
- 그래프 이론
- DP
- SW Expert Academy
- 파이썬
- javascript
- 자바스크립트
- 너비 우선 탐색
- 구현
- 너비우선탐색
- 문자열
- 백준 알고리즘
- 스택
- 그리디 알고리즘
- 다이나믹 프로그래밍
- 이분 탐색
- DFS
- 데이터베이스
- 완전탐색
- 프로그래머스
- Today
- Total
민규의 흔적
[C++] 백준 1300번 - K번째 수 본문
2025년 5월 16일
문제 링크 : 백준 1300번 - K번째 수
문제 접근
문제는 정말 간단한다. (이런 간단한 문제가 정말 무서운 문제다.)
N 이 3이라면 3X3 사이즈의 A 행렬은 다음과 같이 나타낼 수 있다.

i 행 j 열의 값은 i * j 로 채워져 있다.
이를 1 X N ^2 사이즈의, A 행렬의 각 요소를 오름차순으로 정렬한 B 벡터는 다음과 같이 나타낼 수 있다.

문제에서 원하는 바는 어떤 정수 k가 주어졌을 때 B[k] 의 값을 구하는 것, 즉 A행렬의 값들 중 k 번째로 작은 값을 구하는 것이다.
( k는 min(10^9, N ^2)보다 작거나 같은 자연수 )
Naive method (시간 초과)
단순하게 생각할 수 있는 방법으로 문제를 다음과 같이 접근해 볼 것이다.
1. A 행렬의 모든 값들을 구한다.
2. 오름차순으로 정렬하여 B 벡터를 구한다.
3. B[k] 값을 도출한다.
분명 위 방법으로 원하는 해를 구할 수 있을 것이다. 시간 제한이 없다면.
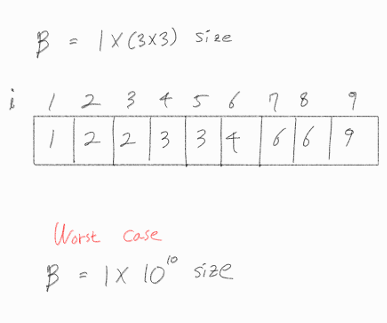
N 은 최대 10^5이다.
A는 최대 (10^5) ^ 2 = 10^10이고, B 벡터는 최대 10^10개의 요소를 가지게 된다.
A 의 요소들을 일일이 계산하는 과정 조차 O(N ^2)이므로 시간초과가 나게 된다.
전체적으로 보아도 O(N ^2) [ A 의 모든 요소 구하기 ] + O(N ^2 lg N) [A 의 모든 요소 정렬하기] 로 시간 제한 안에 풀기엔 어림도 없음을 알 수 있다.
일단 적어도 모든 A 의 요소들을 계산하는 것도 지양해야 하고, 더 나아가 이 값들을 정렬하는 과정 또한 지양해야 한다. (우린 그럴 시간이 없다!)
다른 풀이 (Solution을 고안하게 된 아이디어의 근간)
( Solution만 보고싶으시면 입력 예제로 바로 가셔도 됩니다. )
문제를 곱씹어보면 유추할 수 있는 정보가 존재한다.
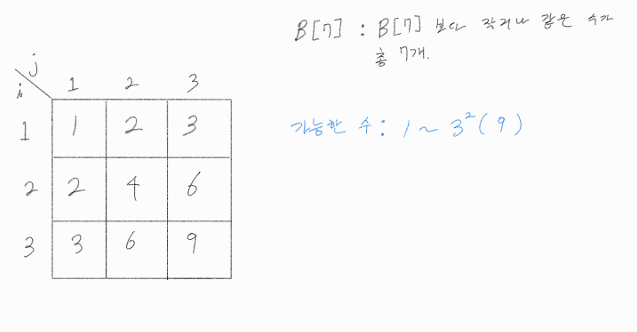
N = 3일 때, B[k] 는 B[k] 보다 작거나 같은 수가 총 k 개라는 뜻이고, B[k] 로 가능한 수는 1 ~ 3^2이다.
또한 B[k] 가 어떤 값 x 라고 가정했을 때, x 가 실제 B[k] 값일 수 있는지 유추할 수 있다.
말이 좀 어려운데 그림을 통해 이해를 돕겠다.
k 가 4라고 가정하겠다. 우리는 B[4] 즉, A 요소들을 오름차순 정렬했을 때 4번째로 작은 수를 알고 싶다.
만약 B[4] = 2라고 가정해보자.

정말 그러할까? 모든 요소를 더하고 정렬해보지 않아도 이는 위를 보면 "맞다" / "아니다" 정도로는 유추가 가능하다.
위 그림을 보면 B[k] = 2인 k 가 존재할 때, k 는 2 또는 3으로 최대 3임을 알 수 있다.
B[k] 가 2가 되려면 k 가 최대 3이어야 한다는 소리다.
이는 "아니다"에 속하며, B[4] 후보가 2보다 커야한다.
그렇다면 B[4] = 3이라고 가정해보면 어떨까?

B[k] = 3일 때, k 는 4 또는 5임으로 최대 5임을 알 수 있다.
여기서 정답이 나왔다. B[k] = 3이 될 수 있는 k 중에 4가 존재하므로, B[4] = 3 자체가 곧 정답이다.

B[k] 값을 x 라고 가정했을 때, k 가 될 수 있는 값이 원하는 값보다 작다면 x 를 늘려주고, 원하는 값보다 크다면 해당 x 를 더 줄여보며 최적해 x 를 구하는 방식으로 문제를 해결할 수 있으리라 짐작된다. 여기에 이분 탐색을 활용하면 x 값을 O(lg N) 시간에 유추할 수 있을 것이다.
하지만 위와 같은 방법은 사실상 매 x 마다 x 보다 작은 요소의 개수를 구하기 위해 요소들을 일일이 다 구해야 하기에 매 유추해보는 x 마다 시간복잡도 O(N^2)이 필요하게 된다.
시간복잡도를 줄이면서 이분 탐색을 활용하는 효율적인 방법은 입력 예제에서 추가로 설명하겠다.
입력 예제
3
7
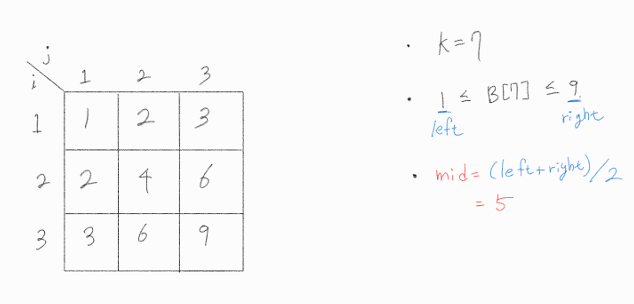
입력 예제를 바탕으로 A 행렬을 나타내면 위와 같다.
B 벡터에 존재할 수 있는 수의 범위는 1부터 3^2인 9까지이다.
따라서 B[7] 의 값은 1 ~ 9 사이에 존재한다.
이제부터 이분 탐색을 수행할 것이다. mid = ( left + right ) / 2 이며, mid 값이 어떤 조건을 만족하냐에 따라 left 혹은 right를 조정할 것이다. 또한 left가 right보다 크거나 같을 때 로직을 종료하며, 이 때 left 값이 문제에서 원하는 해가 된다.
문제 접근의 마지막 부분에서, B[k] 를 x라고 가정했을 때, k에 해당하는 값을 구하기 위해 결국 모든 요소를 일일이 계산해야 한다고 하였다. 하지만 모든 요소를 계산하지 않고, 각 행마다 x 보다 작거나 같은 값이 몇 개인지만 알면 적어도 x 라고 가정했을 때 k 의 최대값 정도는 알 수 있다.
다음 예시를 살펴보자.
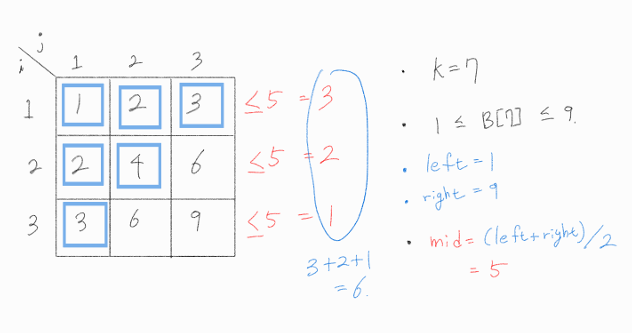
현재 mid는 5이다. B[k] = 5라고 가정한다면 k는 최대 6임을 알 수 있다.
이를 일일이 계산하지 않고 다음과 같이 수행하면 각 행마다 O(1) 시간에 계산해서 k의 최대값을 알 수 있다.

정확히 어느 값이 5보다 작은지는 몰라도, A 행렬의 규칙( 각 i 번째 행의 요소는 i * 1, i * 2, ... , i * N임 ) 을 활용해 각 행에 5보다 작거나 같은 요소가 몇 개 존재하는지는 알 수 있다.
이렇게 하면 A 행렬에 존재하는 모든 요소들 중, 5보다 작거나 같은 요소의 개수를 O(N) 시간에 구할 수 있다.
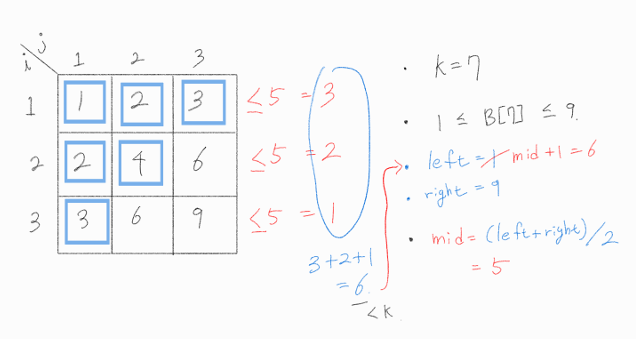
5보다는 작거나 같은 요소가 6개이므로, k = 7보다 작다. 따라서 B[7] 은 5보다는 크다고 추측할 수 있다.
이에 mid 값을 증가시켜보기 위해 left 값을 다음과 같이 mid + 1로 증가시킨다.

B[7] = 7이라고 가정해보자.
그렇다면 아래와 같이 A 행렬에서 7보다 작거나 같은 수가 총 몇 개인지 구할 수 있다.

총 8개이므로, 정확하게 알 수 있는 것은 B[8] 은 7보다 작거나 같다는 것이다.
이는 B[7] 은 최대 7이라는 의미와도 같다. ( 실제 A 행렬에는 7이 존재하지 않지만 최대 7일 것이라고 추측한다. )
그렇다면 B[7] 이 될 수 있는 값들 중, 최소값을 구하고자 mid를 줄이기 위해 다음과 같이 right = mid - 1로 조정한다.
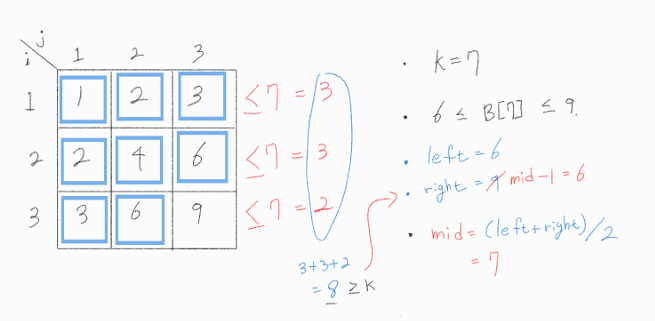
right를 조정하고 보니 아래와 같이 left가 right보다 같아졌으므로 로직을 종료한다.

따라서 B[7] = 6이며, 이는 실제 정답과 비교하여도 정해임을 알 수 있다.
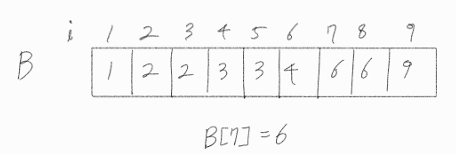
위와 같이 문제를 해결하면 시간복잡도는 O(lg N) [이분 탐색] * O(N) [각 행에 mid보다 작거나 같은 값이 몇 개인지 구하는 연산] = O(N lg N)의 아주 효율적이게 된다.
출력 예제
6
전체 코드
// 1300
#include <iostream>
#define endl "\n"
#define ll long long
using namespace std;
int main(void) {
ll int N, K;
cin >> N >> K;
ll int left = 1;
ll int right = N * N;
while (left <= right) {
ll int mid = (left + right) / 2;
ll int cnt = 0;
for (int i = 1; i <= N; i++) {
cnt += min(N, mid / i);
}
if (cnt >= K) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
cout << left << endl;
}
풀이 후기
문제에서 규칙을 찾아 시간복잡도를 최대한 줄이는 과정에서 어떤 알고리즘으로 연결시킬 수 있고, 결과적으로 얼마나 효율적인 알고리즘을 도출해낼 수 있는지의 척도를 보는 문제였다고 생각한다.
'BOJ' 카테고리의 다른 글
| [C++] 백준 28119번 - Traveling SCCC President (0) | 2025.05.16 |
|---|---|
| [Python 파이썬] 백준 2583번 - 영역 구하기 (0) | 2024.10.02 |
| [Python 파이썬] 백준 1926번 - 그림 (0) | 2024.10.02 |
| [Python 파이썬] 백준 5972번 - 택배 배송 (1) | 2024.09.26 |
| [Python 파이썬] 백준 1283번 - 단축키 지정 (1) | 2024.09.05 |



