| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- DP
- 문자열
- Python
- 너비우선탐색
- BFS
- 파이썬
- 프로그래머스
- 백준 알고리즘
- DFS
- 오라클
- 그래프 이론
- SW Expert Academy
- 자바스크립트
- 그래프 탐색
- 다익스트라
- 이분 탐색
- 브루트포스
- 백트래킹
- 다이나믹 프로그래밍
- 데이터베이스
- oracle
- 백준알고리즘
- C++
- 스택
- 구현
- SWEA
- 브루트포스 알고리즘
- javascript
- 너비 우선 탐색
- 그리디 알고리즘
- Today
- Total
민규의 흔적
[오라클 DB] 관계 대수 연산자 - 일반 집합 연산자 본문
관계 대수 연산자

관계 대수 연산자는 크게 일반 집합 연산자와 순수 관계 연산자로 구분된다.
이 포스팅에선 일반 집합 연산자에 대해 알아보도록 하겠다.
일반 집합 연산자
| 연산자 | 기호 | 표현 | 의미 |
| 합집합 | ∪ | R ∪ S | 릴레이션 R과 S의 합집합을 반환 |
| 교집합 | ∩ | R ∩ S | 릴레이션 R과 S의 교집합을 반환 |
| 차집합 | - | R - S | 릴레이션 R과 S의 차집합을 반환 |
| 카티션 프로덕트 | x | R x S | 릴레이션 R의 각 튜플과 릴레이션 S의 각 튜플을 모두 연결하여 만든 새로운 튜플을 반환 |

피 연산자인 두 릴레이션은 집합 연산이 가능하기 위해 합집합 호환(union compatible)이어야 한다.
합집합 호환 조건
두 릴레이션 R1(A1, A2, ..., An)과 R2(B1, B2, ..., Bm)이 합집합 호환일 필요 충분 조건은
n=m이고, 모든 1<=i<=n에 대해 domain(Ai)=domain(Bi)
즉, 두 릴레이션의 애트리뷰트 수가 같고 각 릴레이션에 대응되는애트리뷰트의 도메인이 서로 동일해야한다.
예를 들어 다음과 같은 릴레이션 스키마가 있다고 가정해보자.
EMPLOYEE(EMPNO, EMPNAME, TITLE, MANAGER, SALARY, DNO)
DEPARTMENT(DEPTNO, DEPTNAME, FLOOR)
위 EMPLOYEE 릴레이션 스키마와 DEPARTMENT 릴레이션 스키마는 합집합 호환인가? 아니다. 두 릴레이션의 애트리뷰트 수가 다르기 때문.
하지만 EMPLOYEE 릴레이션에서 DNO를 프로젝션( π )한 결과 릴레이션인 ' π DNO (EMPLOYEE) ' 과 DEPARTMENT 릴레이션에서 DEPTNO를 프로젝션한 결과 릴레이션 ' π DEPTNO (DEPARTMENT) ' 는 애트리뷰트 수가 같고 DNO와 DEPTNO의 도메인이 같으므로 합집합 호환이다.

합집합(union) 연산자
두 릴레이션 R과 S의 합집합 R ∪ S는 R 또는 S에 있거나 R과 S 모두에 속한 튜플들로 이루어진 릴레이션이다.
형식
∪ 기호 사용

연산 결과
결과 릴레이션에서 중복된 튜플들은 제외된다.
결과 릴레이션의 차수는 R 또는 S의 차수와 같으며, 카디널리티는 릴레이션 R과 S의 카디널리티를 더한 것과 같거나 작다.
결과 릴레이션의 애트리뷰트 이름들은 R의 애트리뷰트들의 이름과 같거나 S의 애트리뷰트들의 이름과 같다.
합집합 예시
질의 : 김창섭이 속한 부서이거나 개발 부서의 부서번호를 검색하시오.
EMPLOYEE 릴레이션
| EMPNO | EMPNAME | TITLE | MANAGER | SALARY | DNO |
| 4377 | 이성래 | 사장 | ^ | 5000000 | 2 |
| 3426 | 박영권 | 과장 | 4377 | 3000000 | 1 |
| 3011 | 이수민 | 부장 | 4377 | 4000000 | 3 |
| 3427 | 최종철 | 사원 | 3011 | 1500000 | 3 |
| 1003 | 조민희 | 과장 | 4377 | 3000000 | 2 |
| 2106 | 김창섭 | 대리 | 1003 | 2500000 | 2 |
| 1365 | 김상원 | 사원 | 3426 | 1500000 | 1 |
DEPARTMENT 릴레이션
| DEPTNO | DEPTNAME | FLOOR |
| 1 | 영업 | 8 |
| 2 | 기획 | 10 |
| 3 | 개발 | 9 |
| 4 | 총무 | 7 |
위 질의에서 김창섭이 속한 부서이거나 (OR) 개발 부서의 부서번호를 검색하여야 하므로 다음과 같은 연산 과정을 거쳐야 한다.
- EMPLOYEE 릴레이션에서 EMPNAME이 김창섭인 튜플을 실렉션한다.
- 해당 튜플의 DNO 애트리뷰트만 프로젝션하여 결과 릴레이션 R1을 도출한다.
- DEPARTMENT 릴레이션에서 DEPTNAME이 개발인 튜플을 실렉션한다.
- 해당 튜플의 DEPTNO 애트리뷰트만 프로젝션하여 결과 릴레이션 R2를 도출한다.
- R1 릴레이션과 R2 릴레이션은 애트리뷰트 수가 1로 같고 도메인도 같으므로(같은 부서번호를 나타냄) 합집합 호환 관계이다. R1 ∪ R2 의 결과 릴레이션을 최종 도출한다.
1~2 과정을 관계 대수 연산자로 표현하면 다음과 같다.

EMPNAME 애트리뷰트 값이 '김창섭'인 튜플을 EMPLOYEE 릴레이션에서 실렉트하면 결과 릴레이션은 다음과 같다.
| EMPNO | EMPNAME | TITLE | MANAGER | SALARY | DNO |
| 2106 | 김창섭 | 대리 | 1003 | 2500000 | 2 |
해당 릴레이션에서 애트리뷰트가 DNO인 값만 프로젝션한 결과 릴레이션 R1은 다음과 같다.
R1
| DNO |
| 2 |
3~4 과정을 관계 대수 연산자로 표현하면 다음과 같다.

DEPTNAME 애트리뷰트 값이 '개발'인 튜플을 DEPARTMENT 릴레이션에서 실렉트하면 결과 릴레이션은 다음과 같다.
| DEPTNO | DEPTNAME | FLOOR |
| 3 | 개발 | 9 |
해당 릴레이션에서 애트리뷰트가 DEPTNO인 값만 프로젝션한 결과 릴레이션 R2는 다음과 같다.
R2
| DEPTNO |
| 3 |
5 과정을 관계 대수 연산자로 표현하면 R1 ∪ R2 이며, 최종 결과 릴레이션은 다음과 같다.
| DNO |
| 2 |
| 3 |
또는
| DEPTNO |
| 2 |
| 3 |
교집합(intersection) 연산자
두 릴레이션 R과 S의 교집합 R ∩ S는 R과 S 모두에 속한 튜플들로 이루어진 릴레이션이다.
형식
∩ 기호 사용

연산 결과
결과 릴레이션에서 차수는 R 또는 S의 차수와 같으며, 카디널리티는 릴레이션 R과 S의 어떤 카디널리티보다 크지 않다.(같거나 적음)
결과 릴레이션의 애트리뷰트 이름들은 R의 애트리뷰트들의 이름과 같거나 S의 애트리뷰트들의 이름과 같다.
교집합 예시
질의 : 김창섭 또는 최종철이 속한 부서이면서 기획 부서의 부서번호를 검색하시오.
EMPLOYEE 릴레이션
| EMPNO | EMPNAME | TITLE | MANAGER | SALARY | DNO |
| 4377 | 이성래 | 사장 | ^ | 5000000 | 2 |
| 3426 | 박영권 | 과장 | 4377 | 3000000 | 1 |
| 3011 | 이수민 | 부장 | 4377 | 4000000 | 3 |
| 3427 | 최종철 | 사원 | 3011 | 1500000 | 3 |
| 1003 | 조민희 | 과장 | 4377 | 3000000 | 2 |
| 2106 | 김창섭 | 대리 | 1003 | 2500000 | 2 |
| 1365 | 김상원 | 사원 | 3426 | 1500000 | 1 |
DEPARTMENT 릴레이션
| DEPTNO | DEPTNAME | FLOOR |
| 1 | 영업 | 8 |
| 2 | 기획 | 10 |
| 3 | 개발 | 9 |
| 4 | 총무 | 7 |
위 질의에서 김창섭 또는(OR) 최종철이 속한 부서이면서(AND) 기획 부서의 부서번호를 검색하여야 하므로 다음과 같은 연산 과정을 거쳐야 한다.
- EMPLOYEE 릴레이션에서 EMPNAME이 '김창섭' 또는 '최종철'인 튜플을 실렉트한다.
- 해당 실렉트 결과 릴레이션에서 DNO 애트리뷰트만을 프로젝션하여 결과 릴레이션 R1을 도출한다.
- DEPARTMENT 릴레이션에서 DEPTNAME이 '기획'인 튜플을 실렉트한다.
- 해당 실렉트 결과 릴레이션에서 DEPTNO 애트리뷰트만을 프로젝션하여 결과 릴레이션 R2를 도출한다.
- R1 릴레이션과 R2 릴레이션의 애트리뷰트 수가 같고 도메인이 같으므로 합집합 호환 관계이다. R ∩ S 의 결과 릴레이션을 최종 도출한다.
1~2 과정을 관계 대수 연산자로 표현하면 다음과 같다.

EMPNAME 애트리뷰트 값이 '김창섭'이거나 '최종철'인 튜플을 EMPLOYEE 릴레이션에서 실렉션한 결과 릴레이션은 다음과 같다.
| EMPNO | EMPNAME | TITLE | MANAGER | SALARY | DNO |
| 3427 | 최종철 | 사원 | 3011 | 1500000 | 3 |
| 2106 | 김창섭 | 대리 | 1003 | 2500000 | 2 |
해당 릴레이션에서 DNO 애트리뷰트 값만 프로젝션하면 결과 릴레이션 R1은 다음과 같다.
R1 릴레이션
| DNO |
| 2 |
| 3 |
3~4과정을 관계 대수 연산자로 표현하면 다음과 같다.

DEPTNAME이 '기획'인 튜플을 DEPARTMENT 릴레이션에서 실렉트한 결과 릴레이션은 다음과 같다.
| DEPTNO | DEPTNAME | FLOOR |
| 2 | 기획 | 10 |
해당 릴레이션에서 DEPTNO 애트리뷰트 값만 프로젝션한 결과 릴레이션 R2는 다음과 같다.
R2 릴레이션
| DEPTNO |
| 2 |
5 과정을 관계 대수 연산자로 표현하면 R1 ∩ R2 이며, R1 릴레이션과 R2 릴레이션 모두에 존재하는 튜플로 이루어진 최종 결과 릴레이션은 다음과 같다.
| DEPTNO |
| 2 |
또는
| DNO |
| 2 |
차집합(difference) 연산자
두 릴레이션 R과 S의 차집합 R - S는 R에는 속하지만 S에는 속하지 않은 튜플들로 이루어진 릴레이션이다.
형식
- 기호 사용
연산 결과
결과 릴레이션의 차수는 R 또는 S와 같으며,
R - S의 카디널리티는 릴레이션 R의 카디널리티와 같거나 적다.
S - R의 카디널리티는 릴레이션 S의 카디널리티와 같거나 적다.
결과 릴레이션의 애트리뷰트 이름들은 R의 애트리뷰트들의 이름과 같거나 S의 애트리뷰트들의 이름과 같다.
차집합 예시
질의 : 소속된 직원이 한 명도 없는 부서의 부서번호를 검색하시오.
EMPLOYEE 릴레이션
| EMPNO | EMPNAME | TITLE | MANAGER | SALARY | DNO |
| 4377 | 이성래 | 사장 | ^ | 5000000 | 2 |
| 3426 | 박영권 | 과장 | 4377 | 3000000 | 1 |
| 3011 | 이수민 | 부장 | 4377 | 4000000 | 3 |
| 3427 | 최종철 | 사원 | 3011 | 1500000 | 3 |
| 1003 | 조민희 | 과장 | 4377 | 3000000 | 2 |
| 2106 | 김창섭 | 대리 | 1003 | 2500000 | 2 |
| 1365 | 김상원 | 사원 | 3426 | 1500000 | 1 |
DEPARTMENT 릴레이션
| DEPTNO | DEPTNAME | FLOOR |
| 1 | 영업 | 8 |
| 2 | 기획 | 10 |
| 3 | 개발 | 9 |
| 4 | 총무 | 7 |
위 질의에서는 말 그대로 소속된 직원이 한 명도 없는, 다시말해 DEPARTMENT 릴레이션의 기본 키인 DEPTNO 애트리뷰트 중, 참조되지 않는 DEPTNO 값을 결과 릴레이션으로 도출하면 된다.
- DEPARTMENT 릴레이션의 DEPTNO 애트리뷰트 값만 프로젝션한 결과 릴레이션 R1을 도출한다.
- EMPLOYEE 릴레이션의 DNO 애트리뷰트 값만 프로젝션한 결과 릴레이션 R2를 도출한다.
- 전체 부서번호 데이터를 가지고 있는 R1 릴레이션에서, 소속된 직원이 한 명이라도 존재하는 부서번호 데이터를 가지고 있는 R2 릴레이션을 차집합 연산 수행을 통해 최종 결과 릴레이션을 도출한다.
1 과정을 관계 대수 연산자로 표현하면 다음과 같다.

해당 연산 결과로 도출된 릴레이션 R1은 다음과 같다.
R1 릴레이션
| DEPTNO |
| 1 |
| 2 |
| 3 |
| 4 |
2 과정을 관계 대수 연산자로 표현하면 다음과 같다.

해당 연산 결과로 도출된 릴레이션 R2는 다음과 같다.
| DNO |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 2 |
| 1 |
결과 릴레이션을 보니 중복되는 튜플들이 존재함을 알 수 있다. 중복 제거를 진행해준 후, 최종 R2 릴레이션을 도출한다.
| DNO |
| 2 |
| 1 |
| 3 |
3 과정을 관계 대수 연산자로 표현하면 R1 - R2 이며, R1 릴레이션에서 R2 릴레이션에 속하지 않는 튜플들로 구성된 최종 결과 릴레이션은 다음과 같다.
| DNO |
| 4 |
또는
| DEPTNO |
| 4 |
카티션 곱(cartesian product) 연산자
릴레이션 R에 속한 각 튜플과 릴레이션 S에 속한 각 튜플을 모두 연결하여 만들어진 새로운 튜플들로 이루어진 결과 릴레이션을 구성한다.
형식
x 기호 사용

연산 결과
카디널리티가 i인 릴레이션 R(A1, A2, ..., An)과 카디널리티가 j인 릴레이션 S(B1, B2, ..., Bm)의 카티션 곱 R ×S는
차수가 n + m이고, 카디널리티가 i*j이고, 애트리뷰트가 (A1, A2, ..., An, B1, B2, ..., Bm)이며,
R과 S의 투플들의 모든 가능한 조합(모든 투플을 각각 연결해 생성된 투플)으로 이루어진 릴레이션
카디션 곱 예시
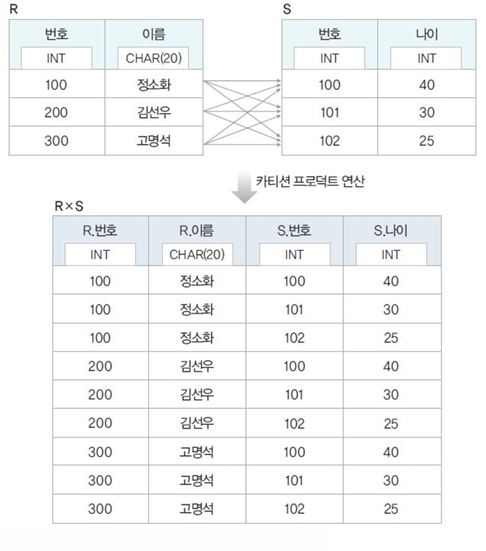
카디널리티가 3이고 차수가 2인 R 릴레이션과 카디널리티가 3이고 차수가 2인 S 릴레이션의 카티션 곱 R x S는
차수가 2 + 2 = 4이고, 카디널리티가 3 * 3 = 9이며
R과 S의 튜플들의 모든 가능한 조합으로 이루어진 결과 릴레이션을 가진다.
'데이터베이스' 카테고리의 다른 글
| [오라클 DB] 질의에 대한 관계 대수식 표현 예제 (0) | 2023.10.18 |
|---|---|
| [오라클 DB] 관계 대수 연산자 - 순수 관계 연산자 (2) | 2023.10.18 |
| [오라클 DB] 관계 데이터 모델과 관계 대수의 기본 개념 (0) | 2023.10.18 |
| [오라클 DB] 무결성 제약조건 (도메인, 엔티티, 참조 무결성 제약조건) (0) | 2023.10.18 |
| [오라클 DB] 릴레이션의 키(키의 종류) (0) | 2023.10.18 |




