| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 다익스트라
- 그리디 알고리즘
- 프로그래머스
- SW Expert Academy
- 문자열
- 그래프 탐색
- 브루트포스
- 너비 우선 탐색
- BFS
- 백트래킹
- 다이나믹 프로그래밍
- 브루트포스 알고리즘
- javascript
- 백준알고리즘
- C++
- 구현
- 백준 알고리즘
- oracle
- 오라클
- 스택
- 파이썬
- 이분 탐색
- 그래프 이론
- 너비우선탐색
- DP
- DFS
- Python
- SWEA
- 데이터베이스
- 자바스크립트
- Today
- Total
민규의 흔적
[Python 파이썬] 백준 17073번 - 나무 위의 빗물 본문
2023년 5월 4일
문제 링크 : 백준 17073번 - 나무 위의 빗물
문제

트리란, 사이클이 없는 연결 그래프를 의미한다. 위 그림은 1번 정점을 루트로 하는 어떤 트리를 나타낸 모습이다.
사실 이 트리는 영훈이가 뒷마당에서 기르고 있는 나무이다. 어제는 비가 왔기 때문에, 트리의 1번 정점에는 W만큼의 물이 고여 있다. 1번 정점을 제외한 모든 정점에는 아직 물이 고여 있지 않은 상태이다.
이제 매초마다 모든 정점은 아래의 작업을 순서대로 반복한다.
- 물을 가지고 있으며, 자식 정점이 있다면 자식 정점 중 하나를 골라 물을 1 준다. 자식 정점이 여러 개라면 동일한 확률로 그 중 하나를 고른다.
- 만약 부모 정점이 자신에게 물을 흘려보냈다면 받아서 쌓아 둔다.
이때, 위 작업은 순서대로 진행되므로 부모 정점에게 받은 물을 즉시 자식 정점에게 줄 수는 없다.
영훈이는 나무를 바라보면서 더 이상 물이 움직이지 않는 상태가 되었을 때 각 정점에 어느 정도의 물이 있게 될지 궁금해졌다. 더 이상 물이 움직이지 않을 때, i번 정점에 쌓인 물의 양의 기댓값을 Pi라 하자. 이때, Pi가 0보다 큰 정점들에 대해서 Pi들의 평균은 어느 정도가 될까?
입력
첫째 줄에 트리의 노드의 수 N과 1번 노드에 고인 물의 양을 의미하는 정수 W가 주어진다. (2 ≤ N ≤ 500,000, 1 ≤ W ≤ 109)
다음 N-1줄에 걸쳐, 트리에 존재하는 간선의 정보가 U V의 형태로 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
이는 양 끝 정점이 각각 U와 V인 간선이 트리에 존재한다는 의미이다.
입력으로 주어지는 트리는 항상 올바른 연결 트리임이 보장되며, 주어지는 트리의 루트는 항상 1번 정점이다.
출력
문제의 정답을 출력한다. 정답과의 차이가 10-3 이하인 값은 모두 정답으로 인정된다.
알고리즘 분류
- 수학
- 그래프 이론
- 그래프 탐색
- 트리
문제 접근
문제를 처음 봤을 땐, 무엇을 원하는 문제인지 감이 안잡혔다. 문제 이해가 안될 땐, 그림을 그려보자!
입력 값은 다음과 같다고 가정하자.
5 5
5 3
3 4
2 1
1 31. 노드의 개수 N : 5, 1번 노드(루트 노드)에 고인 물의 양 W : 5
2. 노드의 연결 관계 (U, V)
위 노드의 연결관계를 트리로 그리면 다음과 같다.

문제에서 물이 흐르는 과정은 다음과 같다고 정의 하였다.
- 물을 가지고 있으며, 자식 정점이 있다면 자식 정점 중 하나를 골라 물을 1 준다. 자식 정점이 여러 개라면 동일한 확률로 그 중 하나를 고른다.
- 만약 부모 정점이 자신에게 물을 흘려보냈다면 받아서 쌓아 둔다.
- 이때, 위 작업은 순서대로 진행되므로 부모 정점에게 받은 물을 즉시 자식 정점에게 줄 수는 없다.
각 단계에 맞춰 '물이 흐르지 않는 상태'의 트리까지 계속 물이 흐르는 과정을 수행 해보자.
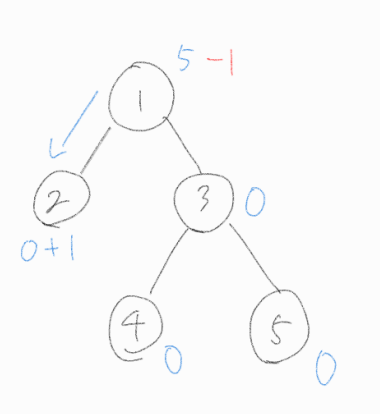
Step 1.
위 과정에 따라 1번 노드는 자식노드 중 하나에게 물을 1만큼 흘려보내야 한다. 자식 노드가 여러 개 라면 동일한 확률로 그 중 하나를 고른다고 했으니, 2번 노드와 3번 노드 중 2번 노드를 택하여 물을 흘려보냈다.
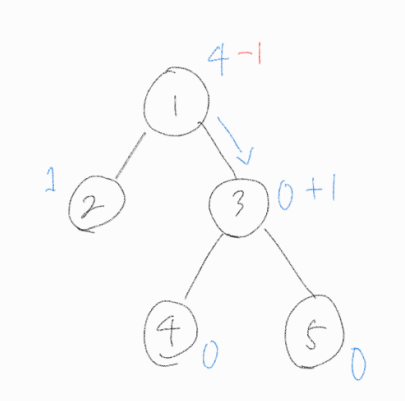
Step 2.
2번 노드는 물이 고여 있으나, 자식 노드가 없기 때문에 정적인 상태를 유지한다.
물이 고여있는 1번 노드는 자식 노드중에 하나를 골라 물을 1 만큼 흘려보내야 하는데, 이번엔 3번 노드로 물을 흘려 보내주겠다.
3번 노드는 물을 받고, 바로 흘려보내는 것이 아닌 일단 잠시 물을 갖고 있는다.
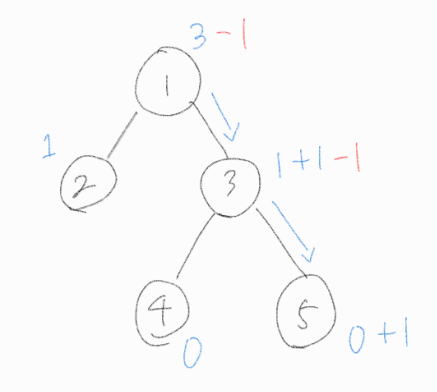
Step 3.
3번 노드는 자식 노드를 가지고 있기에, 4번 노드와 5번 노드 중 한 노드를 골라 물을 1만큼 흘려 보내야 한다. 5번 노드를 택해 물을 흘려주겠다.
그럼과 동시에 1번 노드 또한 물을 가지고 있기에 자식 노드 중 한 노드에게 물을 흘려 보내 주어야 한다. 3번 노드로 1만큼 물을 흘려 보내주겠다.
3번 노드는 받은 물을 일단 가지고 있는다.
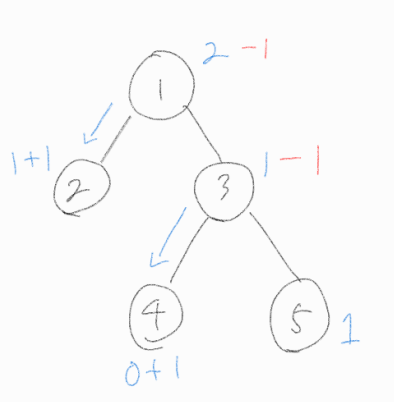
Step 4.
3번 노드는 자식 노드 중, 4번 노드에게 물을 흘려 보내준다.
1번 노드도 아직 물을 가지고 있기에, 자식 노드 중 2번 노드에 물을 흘려 보내준다.
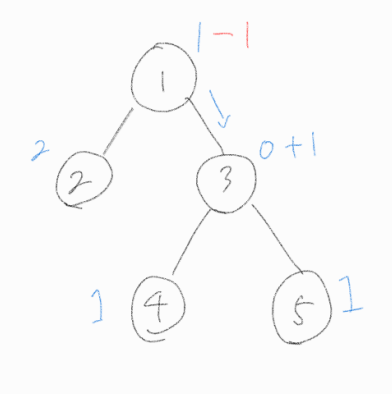
Step 5.
1번 노드는 자식 노드 중, 3번 노드에 물을 흘려 보내준다.
기존에 물을 갖고 있지 않았기에, 3번 노드는 자식 노드에 물을 흘려보내지 않고 1번 노드로부터 받은 물을 가지고 있는다.
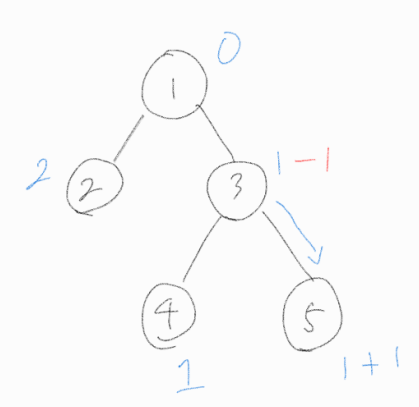
Step 6.
3번 노드는 가지고 있던 물을 자식 노드 중, 5번 노드에 흘려 보내준다.
1번 노드에서 물을 흘려보내주려 했는데, 1번 노드에 더 이상 물이 없기에 추가 작업은 진행되지 않는다.
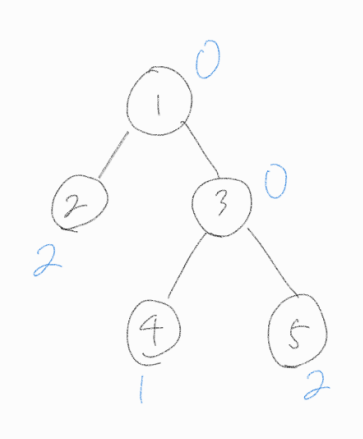
자식 노드를 가지고 있는 모든 노드들은 자식노드에게 물을 전달해 주었기에, 루트노드에 있던 물의 양 5는 해당 트리의 모든 리프노드가 나눠갖게 된다.
이 포인트가 문제의 핵심이라고 할 수 있겠다.
문제가 원하는 출력 값을 한 번 더 확인해보자.
- 더 이상 물이 움직이지 않을 때, i번 정점에 쌓인 물의 양의 기댓값을 Pi라 하자. 이때, Pi가 0보다 큰 정점들에 대해서 Pi들의 평균은 어느 정도가 될까?
Pi가 0보다 큰 정점들에 대해 Pi들의 평균을 구하는 문제이다. Pi가 0보다 클 수 있는 정점은 무엇일까? 리프 노드이다.
이 문제는, 전체 물의 양 W를 주어진 트리의 리프 노드의 개수로 나눈 값이 무엇인지를 묻는 문제이다.
순서도
1. 입력값을 입력받음. tree는 연결리스트로 받는다.
2. 리프노드가 무엇인지 확인 => 연결된 관계가 1개밖에 없다면 리프노드다.
2-1. 허나, 노드가 2개이고, 1 - 2 관계밖에 없는 예외 케이스에서는,
해당 로직에 의하면 루트 노드인 1번 노드 또한 리프노드로 판단해 버린다.
리프노드 확인은 2번 노드부터 진행하도록 한다.
3. 전체 물의 양 W 을 리프노드의 개수로 나누어 출력입력 예제
5 20
5 3
3 4
2 1
1 3
입력 예제 풀이 과정은 문제 접근의 방식과 같다.
출력 예제
6.6666666667
주의할 점
1. 연결리스트로 Tree 선언 후, 리프노드의 여부를 판단하는 방법은 연결되어있는 노드의 개수가 1개 뿐인지 아닌지가 기준이 된다. 허나 입력 노드가 2개(1,2)밖에 없는 경우 루트 노드 또한 연결되어있는 노드가 1개 뿐으로 나타나기에, 루트 노드까지 리프노드로 식별하게 되는 참사가 벌어질 수 있다. 입력 노드가 2개인 경우를 대비해, 리프노드 검사 로직 for문에서는 2번 노드부터 검사하도록 유도한다.
전체 코드
# 17073
'''
문제가 요하는 바 : 자식노드가 있으면 자식노드 중 하나한테 물을 1씩 흘려보냄
= 자식노드를 가지는 노드라면 결국 물의 양이 0이 될 때까지 자식노드로 물을 흘려보낼 것
그렇다면? 최종적으로 모든 리프노드에 물의 전체 양 W가 배분되어 있을 것이다.
내 예상 풀이
1. 입력값을 입력받음. tree는 연결리스트로 받는다.
2. 리프노드가 무엇인지 확인 => 연결된 관계가 1개밖에 없다면 리프노드다.
3. 전체 물의 양 W 을 리프노드의 개수로 나누어 출력
'''
'''
set_tree : 트리를 연결리스트로 생성 및 리턴할 메소드
입력 값 N : 생성할 트리의 노드 개수
리턴 값 tree : 연결리스트로 생성한 트리
'''
import sys
input = sys.stdin.readline
def set_tree(N):
tree = [[] for _ in range(N+1)] # 0번째 인덱스는 더미
for _ in range(N-1):
# tree를 연결리스트 형태로 입력받음
v1,v2 = map(int,input().split())
tree[v1].append(v2)
tree[v2].append(v1)
return tree
'''
get_leafcnt : 트리의 리프노드 개수를 리턴할 메소드
입력 값 tree : 리프노드의 개수를 알고 싶은 tree
리턴 값 leafcnt : 해당 트리의 리프노드 개수
'''
def get_leafcnt(tree):
leafcnt = 0
# 더미 값과 루트노드는 노드 검사에서 제외한다.
'''
N = 2일 경우, 1 - 2 관계가 전부. 각 연결관계는 1개임
해당 로직대로라면 루트노드도 리프노드라고 판단해버림.
그런 상황을 대비하여, 루트노드도 검사에서 제외한다.
'''
for i in range(2,len(tree)):
if len(tree[i]) == 1:
leafcnt += 1
return leafcnt
if __name__ == "__main__":
N,W = map(int,input().split())
# 1. 트리를 입력 받음
# 2. 해당 트리를 get_leafcnt 메소드 파라미터로 대입
# 3. leafcnt에 해당 tree의 리프노드 개수를 받아놓음
leafcnt = get_leafcnt(set_tree(N))
# 4. W / leafcnt 출력
# 루트노드만 존재한다면, leafcnt가 0이 되어 예외가 발생하지만
# 해당 문제에선 노드가 최소 2개이기에 상관 없음.
print(W / leafcnt)
풀이 후기
자식 노드가 있을 때 무조건 자식 노드로 물이 흐른다는 조건이, 결국 리프노드가 물의 양 W를 나눠 가진다는 뜻임을 깨닫는다면 쉽게 풀 수 있는 문제라고 생각한다.
'BOJ' 카테고리의 다른 글
| [Python 파이썬]백준 1477번 - 휴게소 세우기 (2) | 2023.05.08 |
|---|---|
| [Python 파이썬]백준 2566번 - 최댓값 (0) | 2023.05.05 |
| [Python 파이썬] 백준 5430번 - AC (0) | 2023.05.04 |
| [Python 파이썬] 백준 1316번 - 그룹 단체 체커 (0) | 2023.05.01 |
| [Python 파이썬] 백준 2941번 - 크로아티아 알파벳 (0) | 2023.05.01 |



