| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- javascript
- 완전탐색
- 너비우선탐색
- 백트래킹
- 스택
- 다익스트라
- SWEA
- 오라클
- 브루트포스 알고리즘
- 브루트포스
- 프로그래머스
- 그래프 이론
- 이분 탐색
- 백준알고리즘
- BFS
- 데이터베이스
- 구현
- oracle
- 문자열
- 너비 우선 탐색
- DP
- 다이나믹 프로그래밍
- Python
- 그래프 탐색
- 파이썬
- 자바스크립트
- 백준 알고리즘
- 그리디 알고리즘
- SW Expert Academy
- DFS
- Today
- Total
민규의 흔적
[Python 파이썬] 백준 1484번 - 다이어트 본문
2024년 4월 2일
문제 링크 : 백준 1484번 - 다이어트
1484번: 다이어트
성원이는 다이어트를 시도중이다. 성원이는 정말 정말 무겁기 때문에, 저울이 부셔졌다. 성원이의 힘겨운 다이어트 시도를 보고만 있던 엔토피아는 성원이에게 새로운 저울을 선물해 주었다.
www.acmicpc.net
문제
성원이는 다이어트를 시도중이다. 성원이는 정말 정말 무겁기 때문에, 저울이 부셔졌다. 성원이의 힘겨운 다이어트 시도를 보고만 있던 엔토피아는 성원이에게 새로운 저울을 선물해 주었다. 성원이는 엔토피아가 선물해준 저울 위에 올라갔다. “안돼!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! G 킬로그램이나 더 쪘어ㅜㅠ”라고 성원이가 말했다. 여기서 말하는 G킬로그램은 성원이의 현재 몸무게의 제곱에서 성원이가 기억하고 있던 몸무게의 제곱을 뺀 것이다.
성원이의 현재 몸무게로 가능한 것을 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 G가 주어진다. G는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄부터 한 줄에 하나씩 가능한 성원이의 현재 몸무게를 오름차순으로 출력한다. 가능한 몸무게가 없을 때는 -1을 출력한다. 현재 몸무게는 자연수로 떨어지지 않을 수도 있는데, 이런 경우는 제외해야 한다.
알고리즘 분류
- 수학
- 두 포인터
문제 접근
입력값으로 주어진 G는 현재 몸무게 ** 2 - 기억하고 있던 몸무게 ** 2 이다.
여기서, 완전제곱식꼴인 식의 구조를 다음과 같이 바꿀 수 있다.
A**2 - B**2 = (A - B) * (A + B)
위와 같이, G는 특정 두 자연수 X( = A - B) 와 Y( = A + B) 의 곱으로 표현될 수 있어야 한다.
(그런 경우의 수가 없을 경우 -1을 출력)
참고로 X와 Y는 같을 수 없다. X와 Y가 같다면 과거 몸무게가 0이라는 의미이며 문제에는 명시되어 있지 않지만 몸무게가 0인 경우는 존재하지 않다는 것이 전제로 깔려있기 때문.(실제로도 몸무게가 0이면 곤란하다.)
A = 현재 몸무게 , B = 기억하고 있던 몸무게(과거 몸무게)이며,
X = A - B , Y = A + B라고 가정했을 때,
위 식을 바탕으로 다음과 같이 A, B 값을 유도할 수 있다.
B(과거 몸무게) 값 유도
A - B = X
A + B = Y
2B = Y - X
B = (Y - X) / 2
구해진 B 값으로 A 값 유도 가능.
A(현재 몸무게) 값 유도
A - B = X
A = X + B
현재, 과거 몸무게인 A, B 값을 유도하는 식을 구했다. 하지만 여기서 한 가지 간과한게 있다.
바로 G를 곱셈으로 표현할 수 있는 자연수 쌍 X, Y를 구해야 하는 것.
여기서 우리는 무식하게 1 ~ G 사이의 자연수 중 2개씩 모두 곱해보며 G가 되는 수를 구하는 것이 아닌, 두 포인터 기법을 이용해 효율적으로 코드가 수행되도록 유도할 것이다.
순서도
1. 입력값 G를 입력받는다.
2. 1 ~ G 까지의 모든 자연수를 오름차순으로 저장한 배열 arr를 선언한다.
3. 두 포인터 기법을 사용하기 위해, 왼쪽 포인터인 left_point와 오른쪽 포인터인 right_point를 선언한다.
left_point의 초기값은 가장 첫 번째 인덱스인 0, right_point의 초기값은 가장 마지막 인덱스인 G-1로 선언한다.
4. 현재 몸무게로 가능한 값을 담아놓을 result 배열을 선언한다.
5. right_point가 left_point보다 작거나 같으면 반복문 종료
5-1. G를 left_point가 가리키는 값으로 나눴을 때 나머지가 0이라면, right_point를 나눈 값 위치의 인덱스 번호로 단번에 옮긴다.
5-1-1. left_point가 가리키는 값 X와 right_point가 가리키는 값 Y를 통해 현재 몸무게(A)와 과거 몸무게(B)를 구한다.
A와 B 모두 자연수라면 현재 몸무게인 A를 result에 append한다.
5-2. left_point를 1만큼 전진시킨다.
6. result가 비어있다면 -1을 출력한다. 아니라면 result를 오름차순 정렬 후 하나씩 출력한다.
입력 예제
15
현재 몸무게와 과거 몸무게를 유도하는 과정은 단순 수식이니 생략하고, G를 곱으로 나타낼 수 있는 서로 다른 자연수 쌍을 두 포인트 기법으로 알아내는 방법을 알아보자.
이는 위 "순서도"의 5-1, 5-2번 과정과 같다.
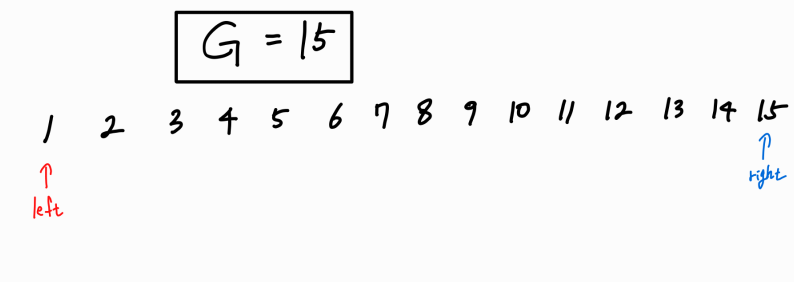
초기 left_point는 배열의 첫 번째, right_point는 배열의 마지막을 가리키고 있다.
우리는 left_point를 기준으로 해당 포인터의 위치는 한 칸씩 옮기되, right_point는 한 칸씩 옮기지 않고 효율적으로 옮길 것이다.
그러기 위해 G를 left_point 값으로 나누어보고, 나머지가 0으로 나눠 떨어지면 나눈 값 위치로 right_point를 옮길 것이다.
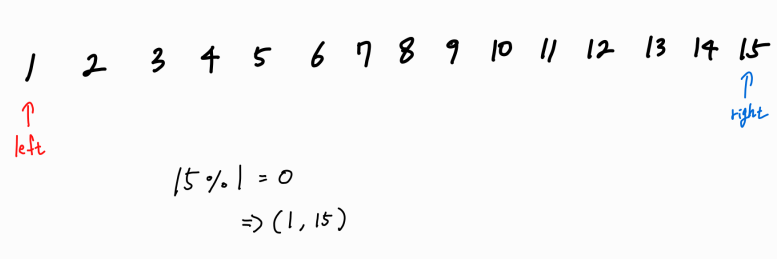
G를 left_point로 나눴을 때 나누어 떨어지니, left_point 값과 G / right_point 값을 한 쌍으로 묶는다.
이후 right_point 위치를 G / right_point 값 위치로 옮겨야 하는데, 이는 현재 위치와 같으므로 움직이지 않는다.
확인이 끝났으니 left_point를 한 칸 옮긴다.

G를 left_point로 나눴을 때 나누어 떨어지지 않는다.
이는 left_point가 가리키는 값 2와 그 어느 자연수의 곱으로도 15를 완성시킬 수 없다는 의미이다.
확인이 끝났으니 left_point를 한 칸 옮긴다.
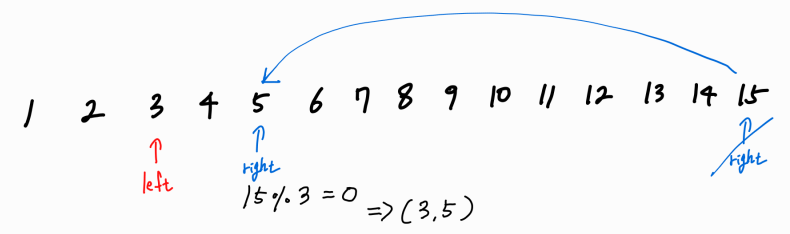
G를 left_point로 나눴을 때 나누어 떨어졌으므로, left_point 값과 G / left_point 값을 한 쌍으로 묶는다.
이후 right_point 위치를 G / right_point 값 위치로 한 번에 옮겨버린다. 원래 있던 자리와 옮긴 자리 사이의 값들은 어느 자연수 조합으로도 불가능하다는 의미이므로 불필요한 연산을 줄일 수 있다.
확인이 끝났으니 left_point를 한 칸 옮긴다.

G를 left_point로 나눴을 때 나누어 떨어지지 않았으므로, 해당 위치 값 4와 그 어느 자연수의 곱으로도 15를 완성시킬 수 없다는 의미이다.
확인이 끝났으니 left_point를 한 칸 옮긴다.
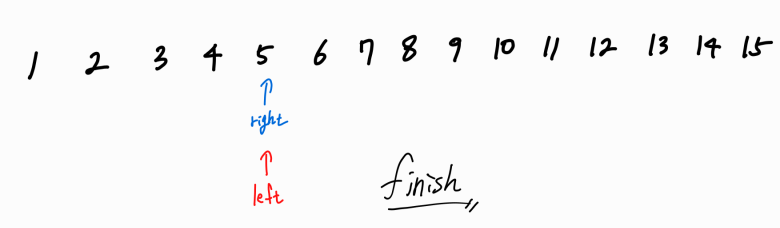
left_point가 right_point와 작을 때 로직을 수행도록 하였기 때문에 연산을 종료하게 된다.
두 포인터가 같은 수를 가리키면 안되는 이유는, 두 수가 같으면 현재 몸무게가 0이 될 수 있기 때문이며
left_point가 right_point를 넘어서면 중복 쌍이 생길 수 있기 때문에(예. (5, 3)) 불필요한 연산이 추가될 수 있다.
따라서 G 값인 15를 곱으로 나타낼 수 있는 1~15 사이의 두 자연수 쌍은 (1, 15) 와 (3, 5)이다.
해당 값을 바탕으로, 위 유도한 수식대로 현재 몸무게가 자연수일 때의 경우를 오름차순으로 출력하면 된다.
출력 예제
4
8
주의할 점
위에서 한 번 언급하였듯, 이 문제에는 명시되어 있지 않지만 몸무게가 0인 경우는 존재하지 않는다는 가정이 존재한다.
과거 몸무게가 0이 되는 경우의 수는 배제해야 한다.
전체 코드
# 1484
def isValid(x, y):
# x <= y
# a - b = x
# a + b = y
# 2b = y - x => b = (y - x) // 2
# a = x + b
b = (y - x) / 2
a = x + b
# a가 정수형으로 떨어지는 경우에만 a 를 return
if int(a) == a:
return int(a)
else:
return -1
def solution():
arr = [i+1 for i in range(G)]
left_point = 0
right_point = G-1
# 답을 담을 배열
result = []
while True:
if G % arr[left_point] == 0:
right_point = (G // arr[left_point]) - 1
# right_point가 left_point보다 작거나 같으면 반복문 종료
if right_point <= left_point:
break
current_weight = isValid(arr[left_point], arr[right_point])
if current_weight != -1:
result.append(current_weight)
left_point += 1
if not result:
print(-1)
else:
result.sort()
for num in result:
print(num)
if __name__ == "__main__":
# G = 현재 몸무게**2 - 이전 몸무게**2 => 인수 분해
# G = (현재 몸무게 - 이전 몸무게) * (현재 몸무게 + 이전 몸무게)
G = int(input())
solution()풀이 후기
두 자연수 쌍을 찾아내는 부분에서, 마치 약수 찾기와 비슷한 느낌으로 두 포인터를 사용하였다.
과거 몸무게가 0이 되면 안되는 점을 뒤늦게 알아내 생각보다 오래 걸린 문제였다.
'BOJ' 카테고리의 다른 글
| [Python 파이썬] 백준 18352번 - 특정 거리의 도시 찾기 (0) | 2024.05.28 |
|---|---|
| [Python 파이썬] 백준 2579번 - 계단 오르기 (0) | 2024.04.11 |
| [Python 파이썬] 백준 2493번 - 탑 (2) | 2023.11.21 |
| [Python 파이썬] 백준 9935번 - 문자열 폭발 (2) | 2023.11.18 |
| [Python 파이썬] 백준 1181번 - 단어 정렬 (0) | 2023.11.18 |



