| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 파이썬
- DP
- 백트래킹
- 다익스트라
- javascript
- SW Expert Academy
- 자바스크립트
- oracle
- Python
- 데이터베이스
- 다이나믹 프로그래밍
- 구현
- 백준알고리즘
- DFS
- 오라클
- BFS
- 브루트포스
- 그래프 이론
- 프로그래머스
- 너비우선탐색
- 그리디 알고리즘
- 스택
- SWEA
- 문자열
- 그래프 탐색
- 백준 알고리즘
- 브루트포스 알고리즘
- 너비 우선 탐색
- 깊이우선탐색
- 완전탐색
- Today
- Total
민규의 흔적
Python 파이썬] SWEA 1220번 - [S/W 문제해결 기본] 5일차 - Magnetic 본문
2024년 5월 8일
문제 링크 : SWEA 1220번 - [S/W 문제해결 기본] 5일차 - Magnetic
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제 접근
N극과 S극을 가진 자성체 모두를 한 칸씩 옮겨보며 진행하자니 테이블의 사이즈가 너무 커(100 X 100) 시간복잡도가 말도 안 될 것이다.
일단 이 문제가 가진 조건들을 하나씩 뜯어보도록 하자.
1. 자성체끼리는 전혀 반응하지 않으며, 테이블 위아래에 존재하는 각 극에만 반응한다.
2. N극 성질을 가지는 1과 S극 성질을 가지는 2가 존재하며, 0은 어느 자성체도 존재하지 않는 칸이다.
3. 각 자성체는 이끌리는 방향으로 계속 끌려가다 배열의 범위를 벗어나면 바닥에 떨어진 것으로 간주된다.
이 3가지 경우를 토대로, S극과 N극 자성체 각각이 서로를 잡아당긴다거나 그런 경우는 존재하지 않으며 각 자성체는 무조건 테이블의 위 또는 아래로 이동하게 될 것임을 알 수 있다.
그리고 가로막힌 장애물이 없다면 각 자성체는 끝까지 이동하다 테이블 밖으로 떨어지게 될 것이다.
여기서 우리는, 100 X 100 사이즈 테이블의 각 열 단위로만 탐색을 진행하면 된다는 것을 알 수 있다.
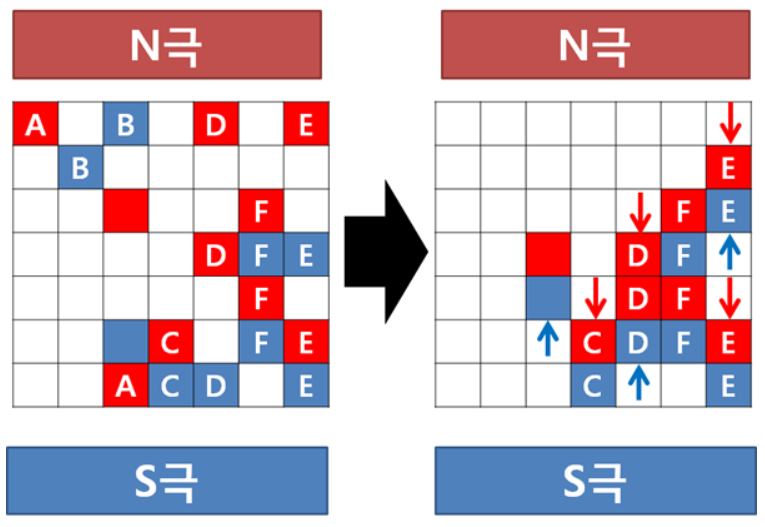
4. 위 그림의 C, D, E, F처럼 각 자성체가 서로 다른 자성체에 의해 진행이 가로막혀 더 이상 움직이 못하는 교착상태 쌍의 개수를 알아야 한다.
5. C, E, F는 각 교착상태 쌍이 각각 1, 2, 2개 존재하며, 예외적으로 D는 한 교착상태에 같은 자성체가 여럿 존재해도 한 쌍으로 간주하여 교착상태 1개로 본다. (N + N + S , N + S + S + S 등 모두 1개로 간주)
이 부분에서, 각 열을 어떻게 탐색해야 2차원 배열을 모두 순회함과 동시에 원하는 결과값을 도출할 수 있는지 알 수 있다.
N극 성질을 가지는 1은 진행 경로가 아래 방향이며, 아래 방향에 진행 경로가 반대인 2 (S극 성질을 지닌 자성체)가 존재한다면 해당 쌍은 교착 상태 쌍이 된다.
그러므로 각 열을 위에서부터 아래 순서로 순회하되, 1(N극)이 존재할 때 그 다음으로 2(S극) 자성체가 존재하면 교착 상태가 일어날 수 밖에 없다는 점을 이용해 문제를 접근해야 한다.
위 그림을 입력 데이터로 보았을 때, 우리는 각 열의 자성체를 담아보며 교착상태인지 확인하기 위한 1차원 배열 stack을 선언해 줄 것이다. ( 위 입력 데이터는 7 X 7 사이즈 이지만 실제로는 100 X 100임에 유의한다. )
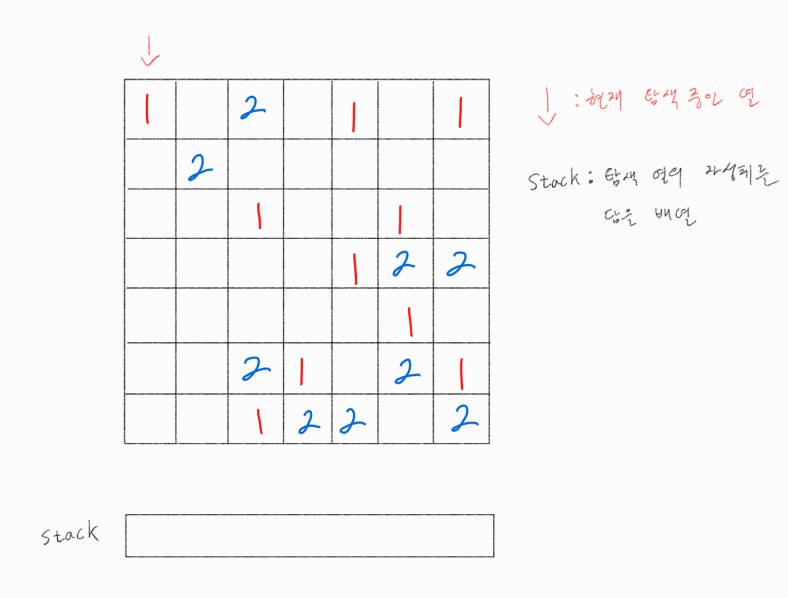
맨 왼쪽 열부터, 각각 열을 위에서 아래 순서대로 탐색을 진행할 것이다.
일단, 교착상태가 되려면 1이 관측된 이후 2가 관측되어야 한다.
2가 먼저 관측되면 가로막는 1이 없기에 테이블 위 방향으로 떨어질 것이기 때문이다.
반대로 1이 관측된 이후 2가 관측되지 않는다면 1은 가로막히지 않기에 테이블 아래 방향으로 떨어질 것이다.
즉, 1이 관측되면 stack에 append 해주고, stack의 마지막 요소가 1일 때 2가 관측되면 이는 교착상태임을 의미하므로 stack을 초기화시키고 교착상태 개수를 1 증가시키면 된다.
1번째 열 탐색

1을 관측한 이후 2를 관측하지 못한 채 탐색이 종료되기에, 교착상태가 존재하지 않는다.
열 탐색이 종료되었으므로 stack을 초기화하여 다음 열을 탐색해보자.
2번째 열 탐색

1을 관측하기 전, 2를 관측했으므로 해당 자성체는 곧장 바닥으로 떨어질 것이다. 이후 아무 자성체도 존재하지 않으므로 탐색을 종료한다.
2번째 열 탐색
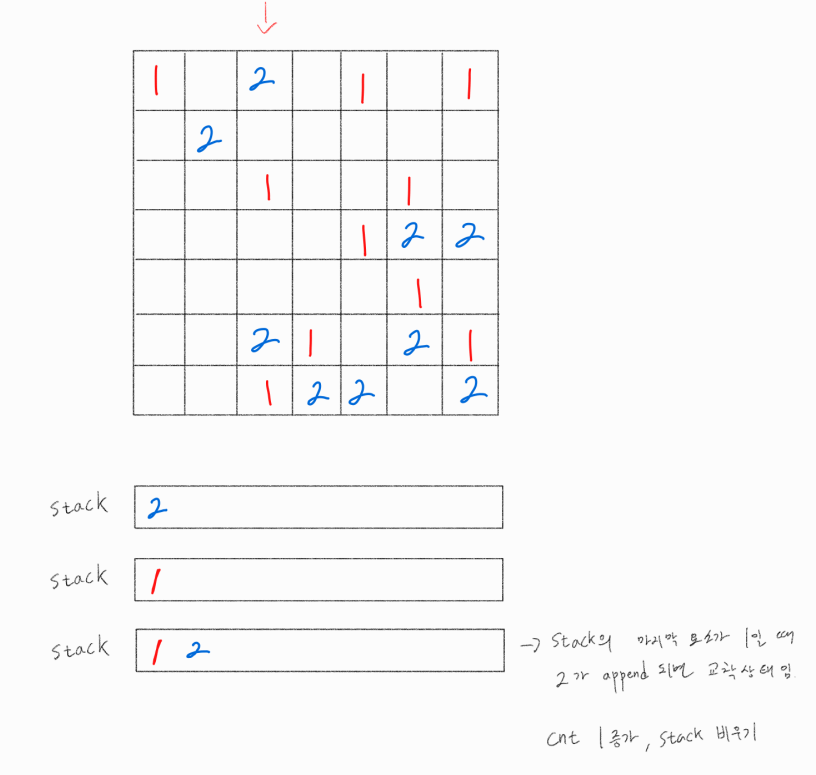
처음 관측된 2는, 이전에 1이 관측되지 않았기 때문에 바닥으로 떨어지게 된다.
이후 관측된 자성체는 1이므로 stack에 append 해주고, 탐색을 더 진행해보니 2가 관측되었다.
1 자성체 다음 2 자성체가 존재한다는 의미는 해당 쌍이 교착상태임을 의미하므로, cnt를 1 증가시키고 stack을 비워준다.

이후 관측된 1은 가로막는 2가 더 존재하지 않기에 바닥으로 떨어지게 된다.
열 탐색이 종료되었으므로 stack을 초기화한다.
3번째 열 탐색
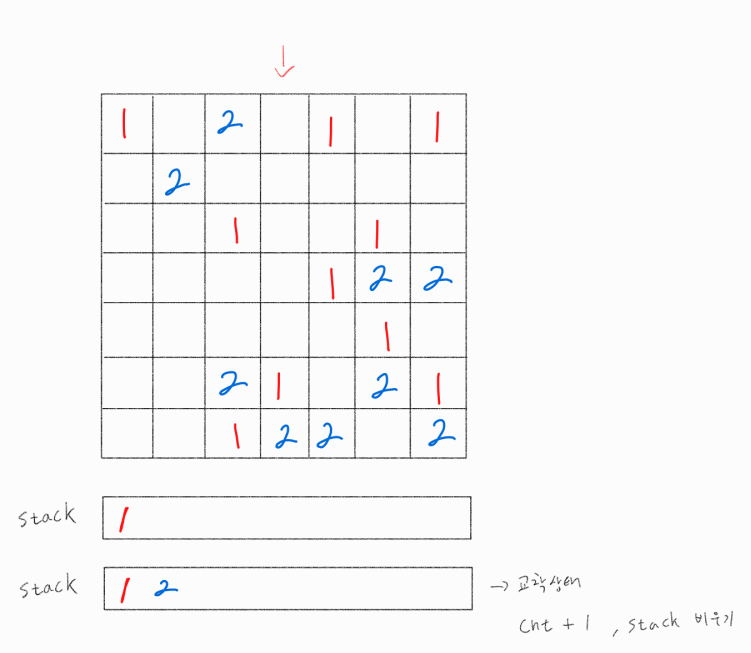
1이 관측되어 stack에 append 해주고, 이후 2가 관측되었으니 해당 쌍은 교착상태로 cnt를 1 증가시키고 stack을 비워준다.
4번째 열 탐색

먼저 1이 관측되었으므로 stack에 1을 append한다.
이후 또 1이 관측되었으므로 stack에 1을 추가로 append한다.
그 이후 2가 관측되었으므로 해당 3개의 자성체는 하나의 교착상태로 간주하여 cnt를 1 증가시키고 stack을 비운다.
해당 로직에서는 stack에 [1, 2], [1, 1, 2] 등 1 다음 2가 관측되는 순간 스택을 초기화해주는데,
만약 [1, 2, 2] 와 같은 순서로 관측되는 상황에서 [1, 2]가 관측되는 순간 stack을 비우기 때문에, 뒤늦게 관측된 2는 stack의 마지막 요소가 1이 아니기에 append해주지 않고 넘겨버린다.
교착 상태를 이루는 자성체의 총 개수를 구하는 문제라면 오류를 범하겠지만, 교착상태의 개수를 구하는 문제이므로 [1, 2]나 [1, 2, 2] 모두 교착상태 하나로 간주하기에 오류를 범하지 않게 된다.
이 점을 기억하고 로직을 이해하면 좋을 듯 하다.
5번째 열 탐색
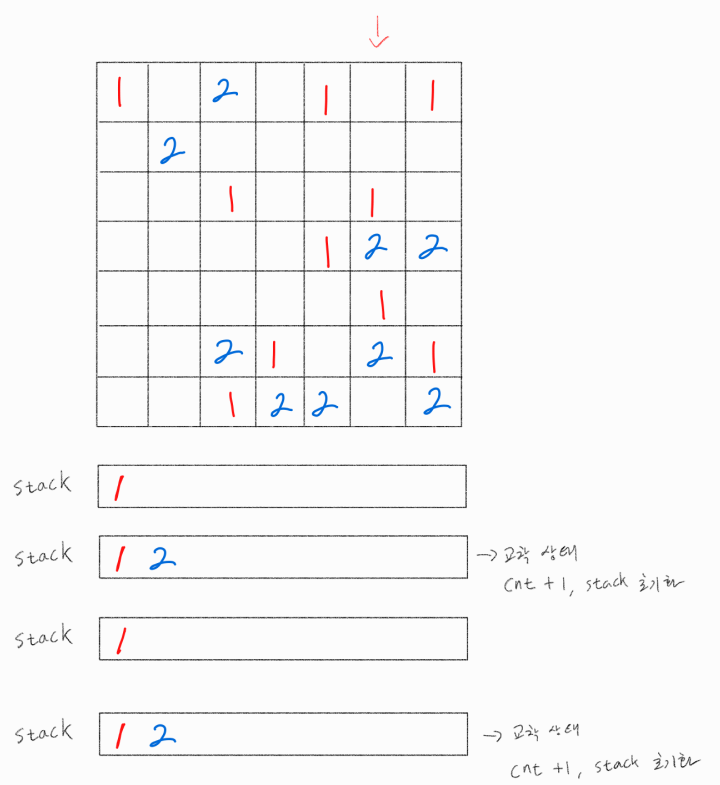
순서대로 1이 관측되어 stack에 append해주고, 이후 2가 관측되어 cnt를 1 증가, stack을 초기화 해주고
또 1이 관측되어 stack에 append해주고, 이후 2가 관측되어 cnt를 1 증가, stack을 초기화 해준다.
6번째 열 탐색
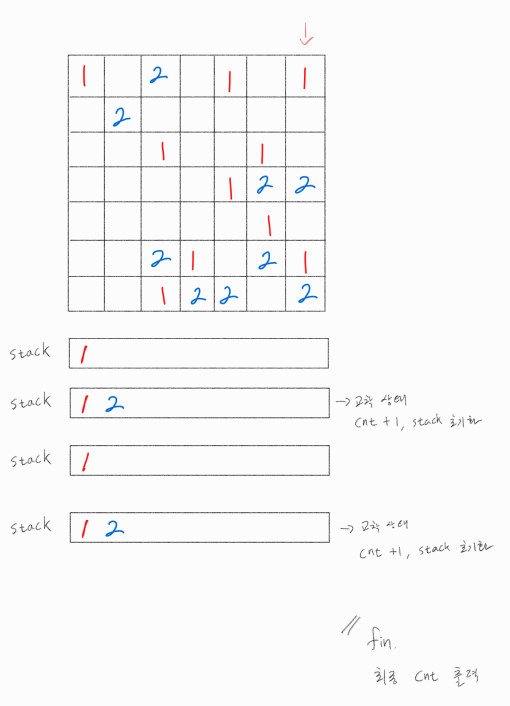
마지막 열 또한 5번째 열 탐색과 같은 로직이 수행되어 cnt를 총 2 만큼 증가시킨다.
마지막 열 탐색이 종료되었으므로 로직을 종료하고, 교착상태 개수인 cnt를 출력한다.
순서도
1. 100 X 100 사이즈의 테이블 board를 2차원 배열 형태로 입력받는다. 교착상태 개수를 담아낼 cnt를 선언한다.
2. board의 각 열을 순서대로 모두 탐색하며, 각 열은 위에서부터 아래 순서대로 탐색한다.
3. 각 열을 탐색하며 관측되는 자성체를 담아낼 stack 배열을 선언한다.
4. 탐색을 진행하며, 1이 관측되면 stack에 append하고, 2가 관측되었을 때에는 stack의 1 요소가 존재한다면 stack을 초기화하고 cnt를 증가시킨다.
5. 로직이 종료되면 cnt를 출력한다.
입력 예제
100
1 0 0 0 0 0 0 0 2 0 0 0 1 0 1 1 0 2 0 0 1 0 2 0 2 2 1 0 0 0 0 0 1 0 0 2 0 0 0 0 0 1 2 0 0 0 1 1...
0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0 0 2 0 0 1 0 0 0 0 0 1 2 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0...
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 2 2 0 2 0 0 0 0 0 1 0 0...
0 0 0 2 0 0 0 0 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 1 0 1 0 0 0 0 0 0 2 0 2 0...
0 0 0 0 2 0 2 0 0 0 2 0 0 0 0 0 0 2 1 1 0 2 0 0 0 1 2 2 2 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0...
0 0 2 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0...
...
100
0 0 0 0 0 0 0 0 0 2 0 0 2 0 0 0 0 0 0 2 0 0 0 1 0 0 0 0 0 0 1 0 2 0 2 0 1 0 1 0 0 0 0 1 0 0 0 0 ...
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 ...
0 0 0 0 2 0 0 0 1 2 1 0 0 0 0 1 0 0 0 0 0 2 0 0 0 0 0 2 2 1 2 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 ...
2 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 1 2 0 2 0 0 0 ...
0 1 1 0 2 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 2 0 0 0 2 0 0 0 0 ...
1 0 0 0 0 1 0 2 0 0 0 0 2 0 2 0 0 0 0 0 0 0 0 0 2 0 0 1 2 0 0 0 0 1 0 0 1 0 0 0 2 0 0 2 2 0 0 0 ...
...
출력 예제
#1 471
#2 446
...
주의할 점
교착상태가 확정되는 조건을 캐치하지 못하고 모든 자성체를 일일이 움직여보는 로직을 구성한다면, 시간초과를 피하지 못할 뿐더러 코드가 상당히 복잡해질 것이다.
전체 코드
def solution():
cnt = 0
board = []
for _ in range(N):
board.append(list(map(int, input().split())))
for col in range(N):
stack = []
for row in range(N):
if board[row][col] == 1:
stack.append(1)
elif board[row][col] == 2:
if stack:
cnt += 1
stack.clear()
return cnt
T = 10
for test_case in range(1, T + 1):
N = int(input())
print(f'#{test_case} {solution()}')
풀이 후기
처음 문제를 접했을 때 ' 어떻게 문제를 풀어야하지...? ' 하고 막막했는데, 손으로 자성체를 움직여보니 명확한 조건이 보여서 생각보다 빨리 풀 수 있었던 문제였다.
'SWEA' 카테고리의 다른 글
| [Python 파이썬] SWEA 11315번 - 오목 판정 (0) | 2024.05.14 |
|---|---|
| [Python 파이썬] SWEA 1860번 - 진기의 최고급 붕어빵 (0) | 2024.05.10 |
| [Python 파이썬] SWEA 1216번 - [S/W 문제해결 기본] 3일차 - 회문2 (0) | 2024.05.10 |
| [Python 파이썬] SWEA 1215번 - [S/W 문제해결 기본] 3일차 - 회문1 (0) | 2024.05.08 |
| [Python 파이썬] SWEA 1289번 - 원재의 메모리 복구하기 (0) | 2024.05.08 |




