| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 너비우선탐색
- 다이나믹 프로그래밍
- 프로그래머스
- 백준 알고리즘
- Python
- javascript
- 이분 탐색
- 문자열
- 스택
- SWEA
- 브루트포스
- 그래프 이론
- 그래프 탐색
- DFS
- 그리디 알고리즘
- SW Expert Academy
- 데이터베이스
- 백준알고리즘
- DP
- 다익스트라
- 파이썬
- 브루트포스 알고리즘
- 구현
- 오라클
- 자바스크립트
- 너비 우선 탐색
- BFS
- oracle
- C++
- 백트래킹
- Today
- Total
민규의 흔적
[Python 파이썬] SWEA 5607번 - [Professional] 조합 본문
2024년 5월 16일
문제 링크 : SWEA 5607번 - [Professional] 조합
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제 접근
문제 자체는 간단하다. N Combination R을 1234567891로 나눈 나머지 값을 구하면 되는 문제.
N combination R을 구하는 수식은 다음과 같다.
N! / R! * (N - R)!
단순히 계산을 통해 정답을 구하려하면 계산 과정에 도출되는 값들이 너무 커질 뿐더러 ( N의 최대값은 1,000,000, 1,000,000!은 상상도 하기 싫은 큰 수이다), 1234567891로 나누기 직전에 도출되는 값은 최대 1,000,000 C 500,000으로 매우 비효율적인 연산 과정을 거칠 것이다.
여기서 우리는 N combination R을 1234567891로 나눈 값을 도출해야 한다는 점에서 모듈러 연산의 특징을 활용할 필요가 있다.
모듈러 연산

a를 n으로 나눈 나머지 값을 a mod n으로 표현할 수 있다.
만약 17 mod 5 라면 해당 값은 2가 될 것이다.
모듈러 합동

임의의 서로 다른 숫자 a, b에 대해 n으로 나눈 나머지 값이 같다면, 모듈러 합동관계(congruent modulo n)라고 한다.
17 mod 5 와 12 mod 5의 값은 모두 2로 같으므로 모듈러 합동관계이다.
이는 17 ≡ 12 mod 5 로 표현할 수 있다.( 17 ≡ 12 (mod 5) )
모듈러 연산의 특징
모듈러 연산의 특징으로는 아래와 같이 3가지가 존재한다.



다시 문제로 돌아와...
N! / R! * (N - R)! 을 1234567891로 모듈러 연산한 값을 알고 싶은 것이니, 다음과 같이 각 연산 과정에 미리 모듈러 연산을 하면 각 연산 결과가 현저히 작아져 연산 속도도 빠를 뿐더러 메모리도 많이 잡아먹지 않을 것이다.
N! mod 1234567891 / ( R! mod 1234567891 * (N - R)! mod 1234567891 )
하지만 애석하게도, 모듈러 연산의 특징에는 나눗셈이 적용되지 않는다.
그렇기 때문에 우리는 분모인 ( R! mod 1234567891 * (N - R)! mod 1234567891 )을 분자로 올리는 과정이 필요하다.
여기서 페르마의 소정리 기법이 사용된다.
페르마의 소정리
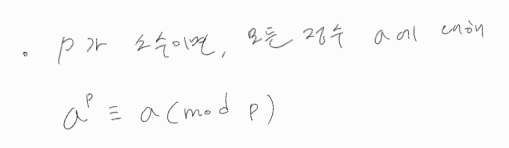
p가 소수일 때, 특정 수 a의 p승을 p로 모듈러 연산한 값은 a를 p로 모듈러 연산한 값과 같다는 정리이다.
여기서 a가 p의 배수가 아니라면 다음과 같은 추가 정리가 더해진다.

p가 71인 소수이고, a가 p의 배수가 아닌 예를 들어 64일 때, 64의 70 - 1승이라는 무지막지하게 큰 값을 71로 모듈러 연산 했을 때, 나머지가 1임을 순식간에 알 수 있는 강력한 정리이다.
위 식은 아래와 같이 표현할 수 있다.

p가 소수이고, a가 p의 배수가 아니라면 a의 -1승( 1/a )을 p로 모듈러 연산한 값은 a의 p-2승을 p로 모듈러 연산한 값과 같다.
다시 문제로 돌아와...
우리는 분모인 ( R! mod 1234567891 * (N - R)! mod 1234567891 )을 분자로 올리는 과정이 필요하다.
분모를 분자로 옮겨 모듈러 곱셈의 분배법칙을 적용시키면 다음과 같이 식이 완성된다.

마지막 줄의 (r! * (n-r)!) ^-1 을 치환해주어야 하는데, r! * (n-r)!을 a로 보면 a^-1이 된다.
어디서 본 적 있지 않은가?
페르마의 소정리에서 본 적 있다!

위 마지막 식에 모듈러 연산의 곱셈 분배법칙을 적용시켜 다음과 같이 식을 정리할 수 있다.

위와 같이 정리가 가능한 이유는 우리가 모듈러 연산하려는 값(1234567891)이 소수이며, a로 치환한 식의 연산 과정이 곱셈 관계이기 때문에 모든 곱 연산마다 1234567891로 모듈러 연산을 하면 계산 결과가 1234567891의 배수가 될 수 없기 때문이다.
위와 같이 정리가 끝났으니, 모든 계산식에 대해 1234567891을 모듈러 연산하여 나타낼 수 있다.
하지만 a를 p-2승만큼 무작정 연산하면 아주아주 오래걸리기에 시간초과를 겪을 수 밖에 없다.
여기서 우리는 분할 정복 기법을 활용해 a의 p-2승을 O(lg N)의 시간복잡도로 구할 것이다.
분할 정복
거듭제곱 식에서 분할 정복을 사용하는 개념은 다음과 같다.
a의 10승은 a의 5승 * a의 5승과 같다.
a의 5승은 a의 2승 * a의 2승 * a의 1승과 같다.
a의 2승은 a의 1승 * a의 1승과 같다.
a를 10번 곱하는 것이 아닌, 위와 같이 3번의 연산으로 분할하여 각 연산 결과를 다시 조립품처럼 맞춰 구하려는 값을 얻어내는 방법이다.
지수가 홀수일 때와 짝수일 때를 구분하여 연산에 주의한다.
a와 b가 존재하고, a의 b승을 구할 때,
1. b가 짝수라면
a의 b승 = a의 b//2승 * a의 b//2승
2. b가 홀수라면
a의 b승 = a의 b//2승 * a의 b//2승 * a의 1승
다시 문제로 돌아와...

우리가 최종적으로 구하고자 하는 식은 위와 같으므로, 각 곱셈식의 값을 따로따로 연산하여 최종적으로 곱한 후 1234567891로 모듈러 연산하면 빠른시간 안에 원하는 결과를 얻을 수 있다.
순서도
1. 모듈러 연산에 이용할 소수인 1234567891을 C에 저장한다.
2. 1! ~ 1,000,000! 값을 담아낼 factorial을 선언한다.
3. factorial[1] 부터 factorial[1,000,000]까지의 값을 차례로 연산하며, 각 값에 C를 모듈러 연산한다.
4. 각 테스트케이스마다 N과 R을 입력 받는다.
4-1. N! mod C 값은 factorial[N]을 통해 값을 얻어낸다.
4-2. R! * (N - R)! mod C 값은 ((R! * (N - R)!) mod C)의 C - 2승이므로 분할 정복을 활용해 값을 얻어낸다.
5. 4-1 값과 4-2 값을 곱하여 C로 모듈러 연산한 값을 출력한다.
입력 예제
1
10 2 // 전체 테스트케이스 개수
// 첫 번째 TC의 정수 N R
출력 예제
#1 45 // 1번 TC의 출력 값
주의할 점
모듈러 법칙, 페르마의 소정리, 분할 정복까지 이해해야 시간 제한 안에 풀 수 있는 문제이다.
전체 코드
'''
분할 정복 기법
X**10 = X**5 * X**5
X**5 = X**1 * X**2 * X**2 ...
지수가 짝수 : 지수를 2로 나눈 몫을 각각 지수로 하는 두 거듭제곱을 곱함
지수가 홀수 : 지수를 2로 나눈 몫을 각각 지수로 하는 두 거듭제곱을 곱하고 밑의 1제곱 수를 다시 곱함
'''
def div_pow(n1, n2):
if n2 == 0:
return 1
ans = div_pow(n1, n2 // 2)
if n2 % 2 == 0:
return (ans * ans) % C
else:
return ((ans * ans) * n1) % C
def solution():
N, R = map(int, input().split())
'''
(n! (mod C)) * ((r! * (n - r)!)^(C - 2)) (mod C))
= (n! (mod C)) * ((r! (mod C)) * ((n - r)!) (mod C))^(C - 2)
a = n! (mod C)
b = (r! (mod C) * (n - r)! (mod C) )^(C - 2)
'''
a = factorial[N]
# (n1 mod m * n2 mod m) mod m = (n1 * n2) mod m
b = div_pow((factorial[R] * factorial[N - R]) % C, C - 2)
return (a * b) % C
T = int(input())
C = 1234567891
factorial = {}
factorial[0] = 1 % C
for i in range(1, 1000001):
factorial[i] = (factorial[i - 1] * i) % C
for test_case in range(1, T + 1):
print(f'#{test_case} {solution()}')
풀이 후기
페르마의 소정리를 이해하는데 상당히 오려걸렸다.. D3가 맞는가 싶었다.
'SWEA' 카테고리의 다른 글
| [Python 파이썬] SWEA 1215번 - [S/W 문제해결 기본] 3일차 - String (0) | 2024.05.14 |
|---|---|
| [Python 파이썬] SWEA 11315번 - 오목 판정 (0) | 2024.05.14 |
| [Python 파이썬] SWEA 1860번 - 진기의 최고급 붕어빵 (0) | 2024.05.10 |
| [Python 파이썬] SWEA 1216번 - [S/W 문제해결 기본] 3일차 - 회문2 (0) | 2024.05.10 |
| Python 파이썬] SWEA 1220번 - [S/W 문제해결 기본] 5일차 - Magnetic (0) | 2024.05.08 |



