| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- SWEA
- 브루트포스 알고리즘
- Python
- 스택
- 프로그래머스
- DP
- 그래프 이론
- 백준 알고리즘
- SW Expert Academy
- 다이나믹 프로그래밍
- C++
- 그래프 탐색
- BFS
- 데이터베이스
- 그리디 알고리즘
- 오라클
- 백준알고리즘
- 구현
- 이분 탐색
- 다익스트라
- 자바스크립트
- 파이썬
- 브루트포스
- 너비 우선 탐색
- javascript
- 백트래킹
- 너비우선탐색
- 문자열
- oracle
- DFS
- Today
- Total
민규의 흔적
[Python 파이썬] 프로그래머스 - 조이스틱 본문
2024년 6월 10일
문제 링크 : 프로그래머스 - 조이스틱
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
시작하기 앞서, 그리디 알고리즘에 대해 간단히 짚고 넘어가겠다. (문제 풀이만 보고 싶다면 아래로 넘어가도 무방하다.)
그리디 알고리즘
탐욕법, 탐욕 알고리즘이라고도 하며, 결과를 도출하기 위해 효율적일 것 같은 방법으로 솔루션을 구하는 알고리즘이다.
최적의 해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
다음 그래프를 보자.

해당 그래프에서 가장 높은 꼭지점이 어디인지 구하고 싶다.
눈으로 보면 어디인지 딱 알 수 있지만, 컴퓨팅적인 사고로 접근하고자 한다.
우리는 다른 지점보다 비교적 상대적으로 높은 지점은 기울기의 절대값이 감소하다 0으로 꺾이는 지점이라고 추측해내 알아낼 수 있다.

시작점이 위와 같다면, 오른쪽 좌표로 계속 이동하며 기울기가 0이 되는 지점을 가장 높은 꼭지점이라고 추측 가능하고, 실제로 이는 정답이 맞다. 모든 지점을 완전 탐색할 필요도 없이 상대적으로 짧은 시간 내에 결과를 도출할 수 있다.
하지만 이는 함정이 있다.

시작점이 위와 같다면, 똑같이 로직을 수행했을 때 도달한 꼭지점을 가장 높은 꼭지점이라고 추측할 수 있지만 이는 실제 해답과는 다르다.
이렇기 때문에 탐욕적으로 접근하며 정답을 도출할 수 있을 것 같으면서도 함정에 빠질 수 있기에 여러 조건을 고려하며 접근해야 하기에 주의해야 한다.
문제 풀이 전에 이를 먼저 설명하는 이유는, 이번 문제가 딱 이런 함정에 빠지기 쉬운 문제라고 생각되어서이다.
문제 접근
여러 조건들을 보며 접근해보자
1. 문자열에 A가 없는 경우
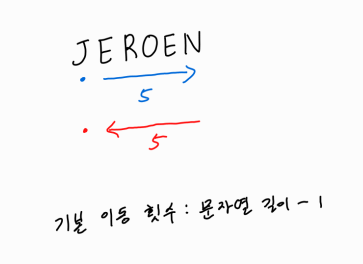
초기 문자열은 모두 A로 세팅되어 있기 때문에, 내가 완성하려는 문자에 A가 없다면 그냥 앞으로든 뒤로든 한 칸씩 이동하며 수정해주면 된다.
여기서 1차적으로 탐욕적인 접근이 사용된다.
내가 맞추려는 알파벳이 A에서 정방향으로 움직여 바꾸는 게 더 빠른지,
아니면 역방향으로 움직여 바꾸는 게 더 빠른지
만약 A 에서 P로 바꾸고 싶다면, 정방향으로 바꿨을 때 15번 조이스틱을 위로 움직여줘야 하지만,
역방향으로 바꾼다면 11번 조이스틱을 아래로 움직여주면 된다.
만약 내가 완성하려는 문자에 A가 있다면 어떻게 해야하는가?
2. 문자열에 A가 존재하는 경우

중간에 A가 있다면, 어차피 바꿔줄 필요가 없는 문자이므로 A를 거쳐가는 것은 손해일 수 밖에 없다.
여기서 우리는 A를 피하는 경로를 찾아야 최소 이동 횟수를 구할 수 있으리라 짐작할 수 있다.
다음과 같은 경우를 보자.

위와 같이 완성시키고자 하는 문자열 중간에 A로만 이루어진 부분 문자열이 존재한다.
이 문자열에 대해 최소 이동 횟수는 크게 2종류 존재하며,
A 군집을 피하지 않는 ①, A 군집을 피하는 ②, ③으로 총 3가지의 탐색 순서가 존재한다.
① : 정방향 완전 탐색(기본 이동 횟수)
② : 시작점에서 A 군집 시작점 바로 왼쪽까지 먼저 탐색 후, 역방향으로 A 군집 끝점 바로 오른쪽까지 탐색
③ : 시작점에서 A 군집 끝점 바로 오른쪽까지 먼저 탐색 후, 정방향으로 A 군집 시작점 바로 왼쪽까지 탐색
① ~ ③의 방법으로 모든 이동 횟수를 구한 후, 최소값을 도출하면 된다.
이를 수식으로 옮기면 다음과 같다.

left = A 군집 시작점 바로 왼쪽 인덱스
(최소값 0. 이유는 최초 탐색의 시작점은 0번 인덱스이기 때문)
right = A 군집 끝점 바로 오른쪽 인덱스
(최대값 length. 이유는 A 군집이 문자열 마지막까지 이어질 경우, 문자열 마지막을 탐색하러 되돌아가는 경우를 차단하기 위함)
length = 문자열 길이
그렇다면, 위 수식이 모든 경우에 예외 없이 옳을 수 있을까?
예외가 모두 적용되는 문자열을 확인해보자.
3. 문자열에 A 군집이 다량 존재하는 경우, A 군집이 문자열의 끝에 존재하는 경우
AAABBBAAAA 처럼, A 군집이 2개 이상 존재하며 문자열의 양 끝에 존재하는 엣지케이스를 고려해주어야 한다.
결론부터 말하면 위 수식을 그대로 옮겨도 문제가 생기지 않는다.
이유는 A 군집을 피하며 탐색한다에 초점을 두었기 때문.
다만, A 군집이 몇 개 존재할 지 모르니, 전체 문자열에 A 군집이 존재할 때마다 최소 이동 거리를 모두 확인하며 갱신시켜주어야 한다.
아래의 예시를 보자.

첫 번째 A 군집을 확인했고, left와 right를 지정해주었다.
A 군집 시작점의 왼쪽은 -1 아닌가? 싶지만, 무조건 탐색의 시작점은 0번 인덱스이기에 left의 최소값은 0이어야 한다.
(A 군집을 피하는것이 목적이지만, 스폰 지점이 A 군집 안이라면 어쩔 수 없다라고 이해하면 편하다.)

두 번째 A 군집에 대해 확인했고, left와 right를 지정해주었다.
A 군집 끝점의 오른쪽은 0이 아닌가? 싶지만, 저런 경우 역방향 탐색으로 문자열 맨 끝으로 탐색하러 이동하는걸 방지하기 위해 right를 끝점 + 1로 지정해주는게 옳다. 저렇게 하면 위 수식에서 볼 수 있듯이 갈 필요 없는 탐색을 원천 차단해준다.
두 번의 이동 횟수 연산을 통해 최소 이동 횟수는 두 번째 A 군집을 피하는 ③ 방법이라는 것을 알아냈다.
결과 도출
모든 문자열을 최소한의 상/하 조작을 통해 바꿔주는 총 횟수 + 최소한의 좌/우 조작을 통해 이동하는 횟수가 우리가 원하는 결과이다.
전체 코드
# 위로 혹은 아래로 조이스틱 움직여서 어디가 더 가까운지 탐색
def now_alpha(target):
return min(ord(target) - ord("A"), ord("Z") - ord(target) + 1)
def solution(name):
answer = 0
length = len(name)
# 연속된 A의 시작점 왼쪽 인덱스
left = 0
move = length - 1
while left < length:
# left를 한 칸씩 옮기며 탐색하니, 탐색하는 김에 상/하 조작 회수 카운트
answer += now_alpha(name[left])
# 연속된 A의 끝점 오른쪽 인덱스
right = left + 1
while right < length and name[right] == "A":
right += 1
# 현재 연속된 A 문자열을 피하면서, 나머지 문자들을 탐색하는 최소한의 횟수
move = min(move, left * 2 + length - right, (length - right) * 2 + left)
left = right
answer += move
return answer
if __name__ == "__main__":
name = "AAABBBAAAA"
print(solution(name))풀이 후기
각 문자를 최소한의 상/하 조작으로 바꾸는 것은 확실하게 그리디한 접근이 가능했으나,
좌/우 조작의 최소값을 찾는 데에서는 함정에 빠지기 쉬운 그리디 알고리즘이 유도됐다고 생각한다.
함정에 빠지지 않기 위해서는 A 군집을 피하는 것이 효율적인 확률이 높다는 탐욕적 사고 + A 군집의 크기가 어떨지 모르니 3가지 탐색 방법을 모두 고려 + A 군집이 몇개일 지 모르니 모든 A 군집에 대한 탐색을 진행해야 하는, Lv2 문제라고 하기엔 조금 어려운 문제였다고 생각한다.
'프로그래머스' 카테고리의 다른 글
| [Python 파이썬] 프로그래머스 - 구명보트 (0) | 2024.06.11 |
|---|---|
| [Python 파이썬] 프로그래머스 - 큰 수 만들기 (0) | 2024.06.10 |
| [Python 파이썬] 프로그래머스 - 타겟 넘버 (0) | 2024.06.08 |
| [Python 파이썬] 프로그래머스 - 괄호 변환 [2020 KAKAO BLIND RECRUITMENT] (0) | 2024.06.08 |
| [Python 파이썬] 프로그래머스 - 줄 서는 방법 (0) | 2024.06.07 |




