| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백준 알고리즘
- SWEA
- 백트래킹
- 그리디 알고리즘
- oracle
- Python
- 자바스크립트
- 그래프 탐색
- 깊이우선탐색
- 프로그래머스
- 구현
- SW Expert Academy
- 완전탐색
- 파이썬
- DP
- javascript
- 브루트포스
- 백준알고리즘
- 오라클
- 다익스트라
- 너비우선탐색
- 문자열
- BFS
- 너비 우선 탐색
- DFS
- 브루트포스 알고리즘
- 그래프 이론
- 데이터베이스
- 스택
- 다이나믹 프로그래밍
- Today
- Total
민규의 흔적
[Python 파이썬]백준 1253번 - 좋다 본문
2023년 5월 11일
문제 링크 : 1253번 - 좋다
문제
N개의 수 중에서 어떤 수가 다른 수 두 개의 합으로 나타낼 수 있다면 그 수를 “좋다(GOOD)”고 한다.
N개의 수가 주어지면 그 중에서 좋은 수의 개수는 몇 개인지 출력하라.
수의 위치가 다르면 값이 같아도 다른 수이다.
입력
첫째 줄에는 수의 개수 N(1 ≤ N ≤ 2,000), 두 번째 줄에는 i번째 수를 나타내는 Ai가 N개 주어진다. (|Ai| ≤ 1,000,000,000, Ai는 정수)
출력
좋은 수의 개수를 첫 번째 줄에 출력한다.
힌트
3,4,5,6,7,8,9,10은 좋다.
알고리즘 분류
- 자료 구조
- 정렬
- 이분 탐색
- 해시를 사용한 집합과 맵
- 두 포인터
문제 접근
좋은 수 란 특정 수가 있을 때, 자기 자신을 제외한 서로 다른 두 수의 합으로 해당 특정 수를 표현할 수 있다면, 그 특정 수는 좋은 수라고 한다.
입력받은 숫자 조합이 2, 3, 4, 6, 7, 10이고, 7이 좋은 수인지 확인해 본다고 가정해보자.
결과만 보자면 7은 좋은 수가 맞다. 3 + 4로 표현 가능하기 때문이다.
처음 문제를 보고, 특정 수를 검사할 때 무식하게 모든 수를 싹다 더해보고, 하나의 경우라도 합했을 때 특정 수로 표현이 되면 누적 개수를 늘려가는 방식을 사용해보려 했으나, 대충 로직을 짜봐도 O(N^3)의 시간복잡도가 나와서 허튼 생각 하지 말고 두 포인터 기법을 사용해 보고자 했다.
다음과 같이 접근해보면 어떨까?

(입력 값을 담을 배열은 오름차순으로 정렬해놓는 것을 기본 전제로 깔고 시작한다)
초기 left와 right의 위치는 양 끝점으로 둔다.
위의 경우, left + right가 test인 7보다 크기 때문에, 합산 값을 줄이고자 right를 1만큼 줄였다.

해당 로직대로 수행하다보면, 위와 같이 left나 right가 test 위치의 인덱스와 겹치는 경우가 생긴다.
이는 '자기 자신을 제외한 다른 두 수의 합' 이라는 조건에 부합하지 않으므로, left가 겹친 경우는 left + 1, right가 겹친 경우는 right - 1 처리를 해준 후, 로직을 이어서 수행 해준다

이번 케이스 또한, left + right가 test보다 크기에 right를 1만큼 줄여주어야 한다.
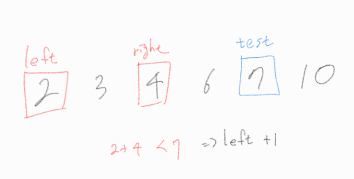
left + right가 test보다 작다. 합산 값을 늘려주어야 하기에, left를 1만큼 늘려준다.

left + right가 test와 같다. 이는 test인 7은 서로 다른 두 수의 합으로 표현 가능하기에 좋은 수임을 밝혀냈다는 뜻이므로, 좋은 수의 개수를 1 누적시킨다.
이 로직으로 문제에 접근할 것이다. 허나 left와 right를 한 칸씩 이동시키는 방식에서 사용할 while문은 어느 조건에서 break를 걸어야 할까?
바로 left와 right가 같아지는 순간이다. "서로 다른 두 수의 합"으로 표현해야 하기에 left가 right를 역전하는 순간에 종료하는게 아닌, 같아진 순간에 종료해야 하는게 그 이유이다.
위 리스트에서 4를 test 해보자. 결론부터 말하자면 4는 좋은 수가 아니다.
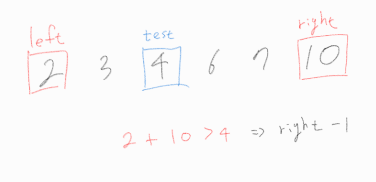
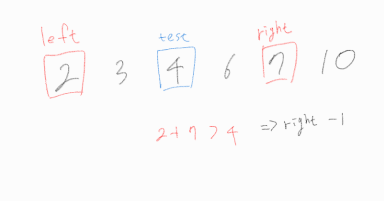
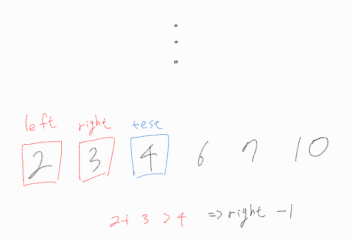
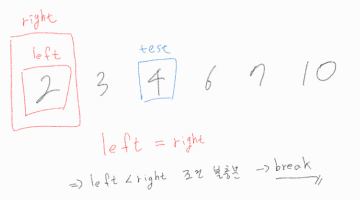
left가 right를 역전 했을 때, 종료하도록 조건을 걸었다면, 해당 경우를 보고 left + right는 4니까 4는 좋은 수구나! 하고 좋은 수 개수를 누적시켰겠지만, 서로 다른 두 수의 합으로 표현 가능해야 하기에, left와 right가 같아진 순간 로직을 종료해야 한다.
나는 여기서 잔머리를 굴려, 수행시간을 조금 더 줄여보고자 다이나믹 프로그래밍 기법을 추가로 사용했다. 잔머리를 굴린 포인트는 다음과 같은 데에서 였다.
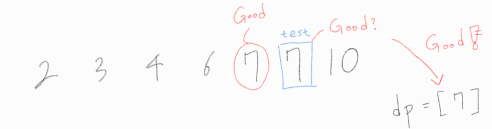
좋은 수임이 확인된 수는 dp라고 선언한 배열에 append 해주고, 다음으로 test하는 수가 dp에 존재하는지, dp에 존재한다면 이미 검증완료 된 좋은 수이기 때문에 로직을 한 번 더 수행할 필요 없도록 유도하는 것이다.
실제로 나처럼 "두 포인터" 기법을 사용한 다른 분들보다 수행시간이 유의미하게 단축되었던 점을 확인할 수 있었다
(아마 운 좋게도 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ..... 같은 입력 예제가 있었나보다)

순서도
1. 입력받은 배열을 오름차순으로 정렬
2. 로직을 수행할 solution() 함수 수행. 매개변수 : "GOOD"인 수가 몇개인지 확인할 리스트
3. 0번째 인덱스 요소부터 '조건에 부합하는 수'인지 확인할 test라는 변수에 대입
3-1 만약 test가 dp에 존재하면, "좋은 수" 개수 + 1 후, 4번 과정 생략하고 다음 요소 test
4. 가장 첫 번째 인덱스 0을 left, 가장 마지막 인덱스 N-1을 right로 가정
4-1 left < right 일 때 까지만 반복문 수행 (left = right까지 허용해버리면, 같은 수 + 같은 수 조합이 생기므로 예외경우 발생)
4-2 left 혹은 right 둘 중 하나가 현재 검사중인 test의 인덱스 위치와 같을 수 있음
4-2-1. left가 test의 인덱스와 같은 경우였다면, left + 1
4-2-2. right가 test의 인덱스와 같은 경우였다면, right - 1
4-3 arr[left] + arr[right] < test인 경우, 수가 left + 1
4-4 arr[left] + arr[right] > test인 경우, right - 1
4-5 arr[left] + arr[right] = test인 경우 "좋은 수" 개수 + 1, dp에 test 추가 후 break
4-5-2. left가 test의 인덱스와 같은 경우였다면, left + 1
4-5-3. right가 test의 인덱스와 같은 경우였다면, right - 1
5. test 위치를 한 칸씩 밀며 4의 과정을 반복 수행
6. 누적된 cnt 출력
입력 예제
10
1 2 3 4 5 6 7 8 9 10
출력 예제
8주의할 점
1. 자기 자신을 제외한 두 수의 합으로 표현가능 하다는 점에서, left와 right가 같아졌을 때 로직 종료해야 함을 이해해야 한다.
전체 코드
import sys
input = sys.stdin.readline
def solution(_arr):
global cnt
global dp
for i in range(N):
test = _arr[i]
# 현재 test할 요소가 dp안에 이미 있는, "좋은 수"라면, 로직 수행하지 말고 cnt + 1, 다음 요소로 건너 뜀
if test in dp:
cnt += 1
continue
left = 0
right = N-1
while(left < right):
# left나 right가 현재 검사중인 test의 인덱스와 같아질 경우, 적절한 조치 후 continue
if left == i:
left += 1
continue
elif right == i:
right -= 1
continue
# left, right가 현재 검사중인 test의 인덱스와 같지 않음이 확인된 이후 로직 수행
else:
# [left] + [right]가 test보다 작다면, 합한 수를 키우기 위해 left + 1
if _arr[left] + _arr[right] < test:
left += 1
# [left] + [right]가 test보다 크다면, 합한 수를 줄이기 위해 right - 1
elif arr[left] + arr[right] > test:
right -= 1
# [left] + [right]가 test와 같다면, dp에 저장 및 cnt + 1
else:
if left != i and right != i: # 자기 자신은 피연산자로 쓰이면 안됨
dp.append(test)
cnt += 1
break
if __name__ == "__main__":
N = int(input())
arr = list(map(int,input().split()))
arr.sort()
dp = [] # 좋은 수를 담을 dp. test할 요소가 dp에 있으면 로직을 반복수행하지 않고 바로 수를 누적시키기 위함
cnt = 0 # "좋은 수"가 몇 개인지 누적시킬 변수
solution(arr)
print(cnt)
풀이 후기
처음에 수를 내림차순으로 정렬하고, 현재 탐색중인 수의 오른쪽 요소들만 부분집합을 따로 떼내어 검사하는 방식으로 수행시간을 줄여보려 했는데, 입력요소에 음수가 섞여있는 케이스에서 로직이 고장나길래 바로 오름차순 정렬 방식으로 방향을 틀고 위와 같이 문제를 풀었다.
'BOJ' 카테고리의 다른 글
| [Python 파이썬]백준 12865번 - 평범한 배낭 (0) | 2023.05.15 |
|---|---|
| [Python 파이썬]백준 2563번 - 색종이 (2) | 2023.05.12 |
| [Python 파이썬]백준 1477번 - 휴게소 세우기 (2) | 2023.05.08 |
| [Python 파이썬]백준 2566번 - 최댓값 (0) | 2023.05.05 |
| [Python 파이썬] 백준 17073번 - 나무 위의 빗물 (0) | 2023.05.04 |




