| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 너비우선탐색
- 백트래킹
- 완전탐색
- 다익스트라
- 브루트포스 알고리즘
- 프로그래머스
- BFS
- 파이썬
- DFS
- 브루트포스
- 너비 우선 탐색
- DP
- 다이나믹 프로그래밍
- 오라클
- javascript
- SW Expert Academy
- 데이터베이스
- 그래프 탐색
- 깊이우선탐색
- SWEA
- 그리디 알고리즘
- Python
- 구현
- 백준 알고리즘
- 스택
- oracle
- 문자열
- 백준알고리즘
- 그래프 이론
- 자바스크립트
- Today
- Total
민규의 흔적
[Python 파이썬]백준 2563번 - 색종이 본문
2023년 5월 12일
문제 링크 : 2563번- 색종이
문제
가로, 세로의 크기가 각각 100인 정사각형 모양의 흰색 도화지가 있다. 이 도화지 위에 가로, 세로의 크기가 각각 10인 정사각형 모양의 검은색 색종이를 색종이의 변과 도화지의 변이 평행하도록 붙인다. 이러한 방식으로 색종이를 한 장 또는 여러 장 붙인 후 색종이가 붙은 검은 영역의 넓이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 색종이의 수가 주어진다. 이어 둘째 줄부터 한 줄에 하나씩 색종이를 붙인 위치가 주어진다. 색종이를 붙인 위치는 두 개의 자연수로 주어지는데 첫 번째 자연수는 색종이의 왼쪽 변과 도화지의 왼쪽 변 사이의 거리이고, 두 번째 자연수는 색종이의 아래쪽 변과 도화지의 아래쪽 변 사이의 거리이다. 색종이의 수는 100 이하이며, 색종이가 도화지 밖으로 나가는 경우는 없다
출력
첫째 줄에 색종이가 붙은 검은 영역의 넓이를 출력한다.
알고리즘 분류
- 구현
문제 접근
가장 먼저 접근했던 방법은 다음과 같고, 결론부터 말하면 틀린데다 코드가 엄청 복잡하고 꼬인다.
- paper라는 빈 배열 선언
- 각 색종이의 시작 꼭지점 [x,y]를 paper 배열에 append함. 최종적으로 paper 배열은 2차원배열이 될 것.
- paper 배열을 탐색하며, 이미 배치한 색종이와 겹친 부분을 연산에서 빼준다
- 최종 검은색 색종이가 차지하는 넓이 출력
위 방법으로 정답을 도출하려면 3번 과정만 수행하면 안 된다.
색종이 2개만 겹치는 부분이라면 빼주기만 하면 되지만, 3개 이상 겹치는 부분은 한 번만 빼면 되는 부분을 또 뺄 가능성이 생기기 때문이다. 보완하려면, 3번 겹친 부분은 겹친 만큼 또 더하고 그 이상 겹치면 빼고 더하고... 오! 머리아파! 이 방법은 잘못된 접근 방법이다!
그러다 문득 생각이 났다. 100 X 100 사이즈의 흰색 도화지를 1 X 1 사이즈의 픽셀이 가로 100개 세로 100개 있다고 생각할 수 있지 않나?
위 방법을 이용한다면, 흰색 도화지를 100 X 100 사이즈의 2차원 배열로 나타낼 수 있고, 색종이가 덧씌워지지 않은 하얀 부분을 0, 색종이가 한 번이라도 덧씌워진 부분은 1로 표시할 수 있을 것이다. 이러면 색종이가 겹치던 말던 신경쓰지 않아도 된다.
마치 흰색 도화지를 여러 단위픽셀로 이루어진 모니터 화면처럼 보자는 것이다.
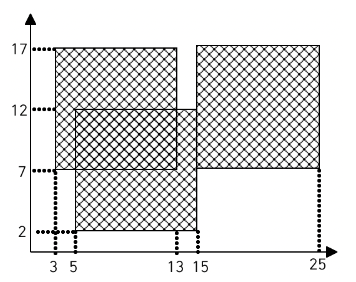
그림을 통해 알아보자.
100 X 100 사이즈의 배열을 표현하기엔 한계가 있어, 10 X 10 사이즈의 도화지라고 가정하고, 색종이의 크기는 모두 3 X 3이라고 임의 정의하겠다.

그림 상단에 조건을 임의 변경하였음을 적었고, 검은색 색종이의 위치 좌표를 각각 [1,1] [2,2] [3,1] 이라고 가정했다.
흰색 도화지는 1 X 1 사이즈의 칸이 가로 10, 세로 10개 존재하다고 표현할 수 있고, 검은색 색종이의 시작 좌표가 주어지면 해당 x 좌표로부터 3칸, y 좌표로부터 3칸만큼 1을 기입해준다.(색종이는 사이즈가 3 X 3 이라고 가정했으니 그렇다) 다른 색종이가 이미 덧씌워져 있어도 상관 없다. 어차피 1번 겹친 부분이나 100번 겹친 부분이나 똑같이 1로 표시되기 때문이다.
위와 같이 나타내면 결국, 색종이를 다 덧씌웠을 때 흰색도화지를 나타내는 2차원 배열에서 1이 몇개 존재하는지만 알아내 출력하면 답이 될 것이다.
순서도
1. 100 X 100 사이즈의 2차원 배열 paper 선언. 각 요소는 0으로 초기화
2. 색종이를 paper에 갖다 댄다고 생각. 해당 색종이가 차지하는 범위를 1로 채움
3. 최종 검은색 색종이가 차지하는 넓이 = paper 배열에서 1의 개수 출력
입력 예제
3
3 7
15 7
5 2
출력 예제
260주의할 점
- 흰색 도화지의 크기는 100 X 100이다. 만약 색종이의 시작 좌표가 [95,95]로 주어진다면, x = 95~105, y = 95~105로 흰색 도화지의 범위를 넘어선다. 이 경우 범위를 넘는 부분은 넓이 계산에서 제외해야 하기 때문, x,y 좌표가 경계점을 넘어가면 1 기입을 멈추도록 해야 한다.
for _x in range(x,x + 10):
for _y in range(y,y + 10):
if _x >= 100 or _y >= 100:
break
paper[_x][_y] = 1아래 전체 코드 중, 위 로직이 주의할 점을 반영한 부분이다.
전체 코드
# 2563
n = int(input())
paper = [[0 for _ in range(100)] for _ in range(100)]
for _ in range(n):
x,y = map(int,input().split())
for _x in range(x,x + 10):
for _y in range(y,y + 10):
if _x >= 100 or _y >= 100:
break
paper[_x][_y] = 1
sum = 0
for row in range(100):
sum += paper[row].count(1)
print(sum)
풀이 후기
흰색 도화지 전체를 1픽셀 단위의 집합처럼 볼 수 있다면 어렵지 않게 풀 수 있는 문제이나, 그렇지 못하면 미궁 속으로 빠지기 쉬운 문제라고 생각한다.
'BOJ' 카테고리의 다른 글
| [Python 파이썬]백준 1759번 - 암호 만들기 (0) | 2023.06.05 |
|---|---|
| [Python 파이썬]백준 12865번 - 평범한 배낭 (0) | 2023.05.15 |
| [Python 파이썬]백준 1253번 - 좋다 (0) | 2023.05.11 |
| [Python 파이썬]백준 1477번 - 휴게소 세우기 (2) | 2023.05.08 |
| [Python 파이썬]백준 2566번 - 최댓값 (0) | 2023.05.05 |



