| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- 브루트포스
- DFS
- 그래프 탐색
- 다이나믹 프로그래밍
- 다익스트라
- BFS
- oracle
- 너비 우선 탐색
- 파이썬
- 오라클
- SWEA
- 백준 알고리즘
- 스택
- 문자열
- 프로그래머스
- 구현
- C++
- SW Expert Academy
- 그리디 알고리즘
- 이분 탐색
- 브루트포스 알고리즘
- Python
- javascript
- 너비우선탐색
- 자바스크립트
- 백트래킹
- 그래프 이론
- DP
- 데이터베이스
- 백준알고리즘
- Today
- Total
민규의 흔적
[오라클 DB] 파일 조직 - 인덱스된 순차 파일, 단일 단계 인덱스 본문
File을 파일 또는 화일이라고 읽는데, 여기서는 파일로 읽겠다.
파일(File) 조직의 유형
- 히프 파일(Heap File)
- 순차 파일(Sequential File)
- 인덱스된 순차 파일(Indexed Sequential File)
- 직접 파일(Hash File)
인덱스된 순차 파일
인덱스를 통해서 임의의 레코드를 접근할 수 있는 파일을 인덱스된 순차 파일이라고 한다.
인덱스 기법으로는 단일 단계 인덱스와 다단계 인덱스로 구분된다.
단일 단계 인덱스
단일 단계 인덱스의 각 엔트리는 <탐색 키, 레코드에 대한 포인터> 쌍 이다.
엔트리들은 탐색 키 값의 오름차순으로 정렬된다.

인덱스는 데이터 파일과는 별도의 파일에 저장된다.
기존 파일의 탐색 키와 각 탐색 키와 동일한 값이 위치한 기존 파일의 레코드들을 가리키는 포인터 값 2개의 쌍이 한 엔트리로 저장된 별도의 파일이다.
따라서 인덱스의 크기는 데이터 파일의 크기에 비해 훨씬 작은 크기를 갖는다.( 차수 : 2 )
또한 하나의 파일에 여러 개의 인덱스들을 정의할 수 있다.
기본 키가 탐색 키의 기본 값이지만, 다른 애트리뷰트들 또한 모두 탐색 키로 지정할 수 있어 기존 파일의 애트리뷰트 수(차수)만큼 인덱스 파일을 정의할 수 있다.

만약 기존 파일의 탐색 키 값이 변경되었다면, 무결성을 지키기 위해 인덱스의 탐색 키 값 또한 변경되어야 한다.
기본 인덱스(Primary Index)
탐색 키가 데이터 파일의 기본 키인 인덱스를 뜻한다.
데이터 파일이 기본 키 순으로 순차 정렬되어 있으며, 테이블마다 최대 한 개의 기본 인덱스만을 가질 수 있다.
데이터 파일을 구성하는 블록 당 하나의 인덱스 엔트리만 포함하며 이를 희소 인덱스라고도 부른다.
따라서 기본 인덱스와 희소 인덱스는 같은 의미이다.
각 인덱스 엔트리는 블록 내의 첫 번째 레코드의 키 값(블록 앵커)을 갖는다.

인덱스 엔트리의 값만 비교해도 특정 값의 위치를 알 수 있다.
예를 들어, 탐색 키가 20인 레코드의 위치를 알고 싶다면, 인덱스 파일의 엔트리 중 탐색 키 값이 10와 30 사이의 위치를 탐색해보면 쉽게 찾을 수 있다.
기본(희소) 인덱스 성능 예시
가정
파일에 레코드가 10,000,000개 있고, 각 레코드의 길이가 200바이트이고, 블록 크기가 4,096 바이트이면 블록킹 인수는 ⌊ 4,096 / 200 ⌋ = 20인 파일을 가정해보자.
이 가정 값들은 위 히프 파일 성능 예시, 순차 파일 성능 예시의 값들과 같다.
데이터 파일의 각 블록마다 하나의 인덱스 엔트리가 인덱스에 들어 있다.
블록 포인터는 4바이트이고, 키 필드의 길이는 20바이트라고 가정하면, 한 인덱스 엔트리의 길이는 24바이트이다.
인덱스 블록킹 인수는 ⌊ 4,096 / 24 ⌋ = 170이므로 인덱스 블록 당 170개의 인덱스 엔트리가 들어간다.
이는 인덱스 블록 당 데이터블록 170개를 가리킨다는 말과 동일하다.
데이터 블록의 개수가 500,000이므로 인덱스의 크기는 ⌈ 500,000 / 170 ⌉ = 2,942 블록이다.
인덱스에서 이진 탐색을 이용하여 하나의 레코드를 찾는데 필요한 블록 접근 횟수는 ⌈ log2 (2,942) ⌉ + 1 = 13이다.
여기서 1은 레코드가 들어 있는 데이터 블록을 접근하는 횟수이다. (DB에서 IO 시간이 가장 오래 걸리기에, 불럭을 읽어오는 횟수를 더해주는 것)
따라서 레코드를 탐색하는데 걸리는 시간은 13 X 10ms = 130ms이다.
(이전 포스팅 글에서 산출한) 순차 파일에서 소요된 시간 190ms와 비교하면 32%만큼 검색 속도가 향상되었음을 알 수 있다.
이는 다단계 인덱스를 통해서 시간을 더 크게 줄일 수 있다.
클러스터링 인덱스(Clustering index)
탐색 키 값을 갖는 데이터 파일은 정렬되어 있어야 하며, 탐색 키 값은 중복 값이 존재할 수 있다.
각 데이터 블록 대신에 각각의 상이한 검색 키 값마다 하나의 인덱스 엔트리가 인덱스에 포함된다.
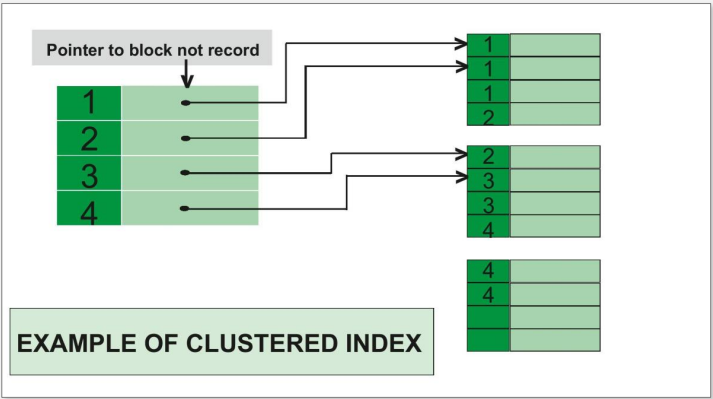
정렬된 데이터 파일의 각각의 탐색 키 값마다 인덱스 엔트리가 존재한다.
인덱스 순서와 물리적 데이터 순서가 일치하기 때문에 데이터를 저장한 블록에 포인터를 저장한다.
한 테이블에 한 개의 인덱스만 생성 가능하다.
위 예시에서 볼 수 있듯이, 탐색 키 값은 정렬되어 있으며 중복되어 있을수 있고, 각 탐색 키가 시작되는 블록의 주소를 포인터로 가리키고 있음을 알 수 있다.
비클러스터링 인덱스(Non-clustering index)
데이터 파일의 레코드들이 탐색 키의 값과 무관하게 저장되어 있으며,
인덱스 순서와 물리적 데이터 순서가 불일치하기 때문에 레코드 각각의 위치를 가리키는 포인터를 저장한다.
정렬되어 있지 않은 필드를 인덱스로 만들겠다는 의미로 재해석 될 수 있다.
한 테이블에 여러 개의 인덱스를 생성할 수 있다.
하나의 데이터 파일에 대해 기본 인덱스는 기본 키를 정렬하며, 그 외엔 모두 비클러스팅 인덱스라고 볼 수 있다.

클러스터링 인덱스 성능 예시
가정
파일에 레코드가 10,000,000개 있고, 각 레코드의 길이가 200바이트이고, 블록 크기가 4,096 바이트이면 블록킹 인수는 ⌊ 4,096 / 200 ⌋ = 20인 파일을 가정해보자.
이 가정 값들은 이전 포스팅 글의 히프 파일 성능 예시의 값들과 같다.
키가 아닌 탐색 키 필드에 인덱스가 정의된다.
총 10,000,000개의 레코드들에 대해 800,000개의 서로 상이한 탐색 키 값(중복을 제거한 서로 다른 값 개수)들이 있다고 가정하자.
또한 인덱스가 정의되는 필드의 길이가 20바이트라고 가정하자.
블록당 인덱스 엔트리 수는 ⌊ 4,096 / 24 ⌋ = 170 이다.
인덱스의 크기는 ⌈ 800,000 / 170 ⌉ = 4,706 블록이다.
인덱스에서 어떤 키 값을 만족하는 첫 번째 레코드를 탐색하는데 필요한 블록 접근 횟수는 ⌈ log2(4,706) ⌉ + 1 = 14이다.
여기서 1은 레코드가 들어 있는 데이터 블록을 접근하는 횟수이다. (DB에서 IO 시간이 가장 오래 걸리기에, 불럭을 읽어오는 횟수를 더해주는 것)
따라서 레코드를 탐색하는데 걸리는 시간은 14 X 10ms = 140ms이다.
보조 인덱스(Secondary index)
한 데이터 파일은 기껏해야 한 가지 필드들의 조합에 대해서만 정렬될 수 있다.
이는 하나의 테이블에 오직 하나의 기본 인덱스만 가질 수 있다는 의미이다.
기본 인덱스가 존재하는 상태에서 다른 탐색 키에 대해 생성한 것을 보조 인덱스라고 한다.
탐색 키 값에 따라 정렬되지 않은 데이터 파일에 대해 정의된다.
인덱스 순서와 물리적 데이터 순서가 불일치하기에 레코드 각각의 위치를 가리키는 포인터를 저장한다.
데이터 파일을 구성하는 레코드당 하나의 인덱스 엔트리를 포함하며, 이는 밀집 인덱스라고도 표현한다.
보조 인덱스는 일반적으로 밀집 인덱스이므로, 같은 수의 레코드들을 접근할 때 보조 인덱스를 통하면 기본 인덱스를 통하는 경우보다 디스크 접근 횟수가 증가할 수 있다.

탐색 키가 중복되어 있으며, 탐색 키가 정렬되어 있지 않기 때문에 모든 레코드를 가리키는 포인터를 저장하는 것을 알 수 있다.
희소 인덱스와 밀집 인덱스 비교
| 희소 인덱스 | 레코드 일부 (블록마다 한 개) 키 값에 대해서만 인덱스에 엔트리를 유지하는 인덱스 (포인터가 각 블록을 가리킨다.) 정렬되어 있다. 레코드의 길이가 블록 크기보다 훨씬 작은 일반적인 경우에는 밀집 인덱스의 엔트리 수보다 훨씬 적다. 희소 인덱스는 일반적으로 밀집 인덱스에 비해 인덱스 단계 수가 1정도 적어 인덱스 탐색 시 디스크 접근 수가 1만큼 적을 수 있다. 오버헤드(삽입/삭제)가 작다. |
| 밀집 인덱스 | 각 레코드의 키 값에 대해서 인덱스에 엔트리를 유지하는 인덱스 (포인터가 각 레코드를 가리킨다.) 정렬되어 있지 않다. 레코드의 길이가 블록 크기보다 훨씬 작은 일반적인 경우에는 희소 인덱스의 엔트리 수보다 훨씬 많다. 밀집 인덱스는 일반적으로 희소 인덱스에 비해 인덱스 단계 수가 1정도 더 많아 인덱스 탐색 시 디스크 접근 수가 1만큼 많을 수 있다. 오버헤드(삽입/삭제)가 크다. |
(오버헤드 Overhead : 어떤 처리를 하기 위해 들어가는 간접적인 처리 시간 · 메모리 등)
희소 인덱스는 밀집 인덱스에 비해 모든 갱신과 대부분의 질의에 대해 더 효율적이다.
하지만 인덱스가 정의된 애트리뷰트만을 검색(예. COUNT 질의)하는 질의는 인덱스만을 접근해서 질의를 수행할 수 있으므로 밀집 인덱스가 희소 인덱스보다 유리한 예외도 존재한다.
또한, 한 파일은 한 개의 희소 인덱스와 다수의 밀집 인덱스를 가질 수 있다.
보조 인덱스(밀집 인덱스) 성능 예시
가정
파일에 레코드가 10,000,000개 있고, 각 레코드의 길이가 200바이트이고, 블록 크기가 4,096 바이트이면 블록킹 인수는 ⌊ 4,096 / 200 ⌋ = 20인 파일을 가정해보자.
이 가정 값들은 이전 포스팅 글의 히프 파일 성능 예시의 값들과 같다.
데이터 파일의 각 레코드마다 하나의 인덱스 엔트리가 인덱스에 들어 있다.
블록 포인터는 4바이트이고 키 필드의 길이는 20바이트라고 가정한다.
한 인덱스 엔트리의 길이는 24바이트이다.
인덱스 블록킹 인수는 ⌊ 4,096 / 24 ⌋ = 170이므로 인덱스 블록당 170개의 인덱스 엔트리가 들어간다.
레코드의 개수가 10,000,000이므로 인덱스의 크기는 ⌈ 10,000,000 / 170 ⌉ = 58,824 블록이다.
인덱스에서 이진 탐색을 이용해 하나의 레코드를 찾는데 필요한 블록 접근 횟수는 ⌈ log2 (58,824) ⌉ + 1 = 17이다.
여기서 1은 레코드가 들어 있는 데이터 블록을 접근하는 횟수이다.(DB에서 IO 시간이 가장 오래 걸리기에, 불럭을 읽어오는 횟수를 더해주는 것)
따라서 레코드를 탐색하는데 걸리는 시간은 17 X 10ms = 170ms이다.
중간에 인덱스의 크기를 보면, 58,824 블록으로 인덱스 파일이 데이터 파일처럼 커진 것을 볼 수 있다.
크기가 커진 인덱스 파일에 대해 또 다른 인덱스 파일을 생성하면 더 빠르게 탐색할 수 있다는 점이 앞으로 알아볼 다단계 인덱스의 기본 접근 방법이다.
정리
- 보조 인덱스는 기본 키 외에 정렬되어있지 않고 중복을 허용하며 이는 비클러스터링 인덱스 혹은 밀집 인덱스와 같은 의미를 지닌다. ( 보조 인덱스 = 비클러스터링 인덱스 = 밀집 인덱스 )
- 기본 인덱스는 기본 키를 탐색 키로 지정하여 정렬되어 있으며 중복을 허용하지 않는다. 희소 인덱스와 같은 의미를 지닌다. ( 기본 인덱스 = 희소 인덱스)
- 클러스터링 인덱스는 탐색 키가 정렬되어 있고 중복을 허용한다.
'데이터베이스' 카테고리의 다른 글
| [오라클 DB] SQL의 인덱스 정의문, 인덱스의 장점과 단점 (0) | 2023.11.20 |
|---|---|
| [오라클 DB] 다단계 인덱스 (2) | 2023.11.20 |
| [오라클 DB] 파일 조직 - 히프 파일, 순차 파일 (2) | 2023.11.14 |
| [오라클 DB] 릴레이션 분해와 정규형(Normal Form) (2) | 2023.11.01 |
| [오라클 DB] 릴레이션 분해와 결정자, 함수적 종속성 (2) | 2023.11.01 |



