| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 백준 알고리즘
- 브루트포스 알고리즘
- DP
- Python
- 이분 탐색
- 스택
- 너비우선탐색
- 프로그래머스
- 파이썬
- C++
- 그래프 탐색
- 구현
- 백준알고리즘
- DFS
- 다이나믹 프로그래밍
- 자바스크립트
- 백트래킹
- 브루트포스
- 데이터베이스
- oracle
- 그래프 이론
- 그리디 알고리즘
- SWEA
- 다익스트라
- 너비 우선 탐색
- SW Expert Academy
- 오라클
- javascript
- BFS
- 문자열
- Today
- Total
민규의 흔적
[Python 파이썬] 백준 14889번 - 스타트와 링크 본문
오늘은 스타트링크에 다니는 사람들이 모여서 축구를 해보려고 한다. 축구는 평일 오후에 하고 의무 참석도 아니다. 축구를 하기 위해 모인 사람은 총 N명이고 신기하게도 N은 짝수이다. 이제 N/2명으로 이루어진 스타트 팀과 링크 팀으로 사람들을 나눠야 한다.
BOJ를 운영하는 회사 답게 사람에게 번호를 1부터 N까지로 배정했고, 아래와 같은 능력치를 조사했다. 능력치 Sij는 i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치이다. 팀의 능력치는 팀에 속한 모든 쌍의 능력치 Sij의 합이다. Sij는 Sji와 다를 수도 있으며, i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치는 Sij와 Sji이다.
N=4이고, S가 아래와 같은 경우를 살펴보자.

예를 들어, 1, 2번이 스타트 팀, 3, 4번이 링크 팀에 속한 경우에 두 팀의 능력치는 아래와 같다.
- 스타트 팀: S12 + S21 = 1 + 4 = 5
- 링크 팀: S34 + S43 = 2 + 5 = 7
1, 3번이 스타트 팀, 2, 4번이 링크 팀에 속하면, 두 팀의 능력치는 아래와 같다.
- 스타트 팀: S13 + S31 = 2 + 7 = 9
- 링크 팀: S24 + S42 = 6 + 4 = 10
축구를 재미있게 하기 위해서 스타트 팀의 능력치와 링크 팀의 능력치의 차이를 최소로 하려고 한다. 위의 예제와 같은 경우에는 1, 4번이 스타트 팀, 2, 3번 팀이 링크 팀에 속하면 스타트 팀의 능력치는 6, 링크 팀의 능력치는 6이 되어서 차이가 0이 되고 이 값이 최소이다.
입력
첫째 줄에 N(4 ≤ N ≤ 20, N은 짝수)이 주어진다. 둘째 줄부터 N개의 줄에 S가 주어진다. 각 줄은 N개의 수로 이루어져 있고, i번 줄의 j번째 수는 Sij 이다. Sii는 항상 0이고, 나머지 Sij는 1보다 크거나 같고, 100보다 작거나 같은 정수이다.
출력
첫째 줄에 스타트 팀과 링크 팀의 능력치의 차이의 최솟값을 출력한다.
알고리즘 분류
- 브루트포스 알고리즘
- 백트래킹
문제 접근
S가 선수들의 능력치이고 한 팀에 1번 선수, 2번 선수, 3번 선수가 존재한다면 해당 팀의 능력치는 다음과 같다.
S[1][2] + S[2][1] + S[1][3] + S[3][1] + S[2][3] + S[3][2]
스타트 팀과 링크 팀에 N명의 선수를 고루 배분했을 때, 능력치 차이가 가장 작을 때의 능력치를 출력하는 문제이다.
팀에 선수를 배정하는 경우의 수를 따져봐야 하므로 백트래킹 기법을 사용하고자 하였다.
다만 여기서 무작정 모든 경우의 수를 구하는 것은 중복되는 연산이 상당히 많아지게 되는데,
나는 4가지 핵심 포인트를 가지고 중복 연산을 최대한 줄이고자 결정하였다.
1. 스타트 팀 조합만 구해도 된다.

스타트 팀과 링크 팀 각각에 배정한 선수가, 팀 명만 상반되고 같은 팀 조합인 경우가 존재한다.
하지만 이는 이번 문제에서 신경쓸 부분이 아니다. 어차피 두 팀의 능력치 차이를 구해야 하므로
1, 2번 선수가 스타트 팀일때 3, 4번 선수가 링크 팀인 케이스와 1, 2번 선수가 링크 팀이고 3, 4번 선수가 스타트 팀인 케이스는 같은 결과를 낳는다는 의미이다.
2. 스타트 팀 인원을 배정하면, 남은 인원은 자동으로 링크 팀이다.
이는 위의 예시를 보면 알듯이, 스타트 팀에게 1, 2번 선수를 배정하면 자동으로 남은 선수는 링크 팀이 된다.
스타트 팀 인원을 배정했다면, 링크 팀 인원을 따로 추가 연산을 통해 배정할 필요는 없다는 것이다.
3. 선수는 오름차순으로 팀에 배정한다.
1, 2번 선수를 스타트 팀에 배정하고 3, 4번 선수를 링크 팀에 배정한 케이스와 2, 1번 선수를 스타트 팀에 배정하고 4, 3번 선수를 링크 팀에 배정한 케이스는 같은 케이스이다.
이러한 중복 연산을 막기 위해 선수를 배정할 때에는 무조건 오름차순으로 배정하도록 하였다.
4. 스타트 팀에 한 명을 고정시켜 놓는다.
결론부터 얘기하면, 한 팀(여기서는 스타트 팀)에 인원 한 명을 고정시키면 중복되는 연산을 상당히 줄일 수 있다.
다음의 예시를 보자
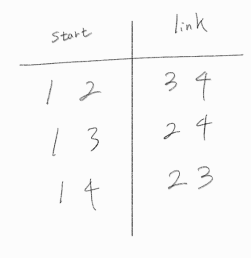


오름차순으로 각 팀에 배정했을 때의 모든 경우의 수이다.
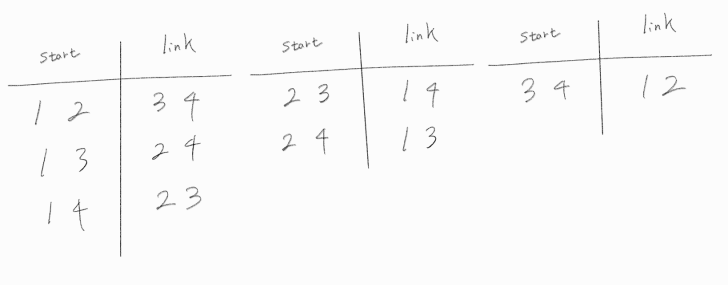
그런데 중복되는 팀이 보인다. 팀 명만 다를 뿐, 궁극적으로 연산 결과는 같아지게 되는 케이스 말이다.

이를 막기 위해선 한 팀에 한 명의 인원을 고정시켜야 한다.
이 방법으로 중복 연산을 줄일 수 있는 이유는 위 1 ~ 3번의 핵심 포인트가 모두 존재하기 때문이다.
입력 예제
4
0 1 2 3
4 0 5 6
7 1 0 2
3 4 5 0
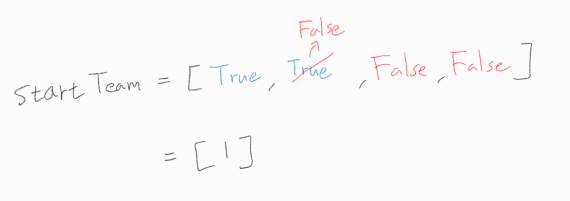
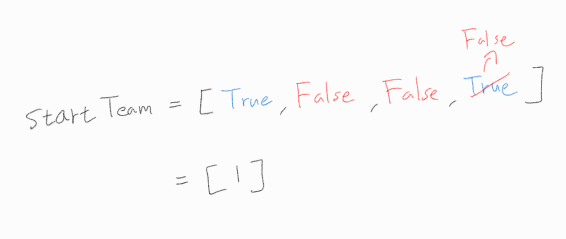
스타트 팀에 배정되어 있는지를 bool 자료형 배열로 표현해보자.
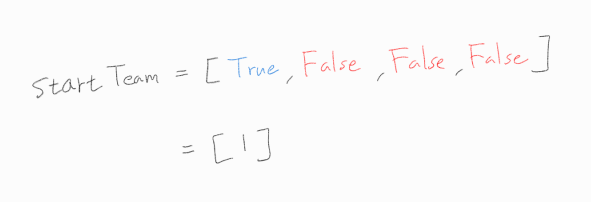
또한, 위의 4번째 핵심 포인트를 바탕으로, 1번 선수를 스타트 팀에 고정시키고 백트래킹을 시작한다.
아래에서 적은 연산이란, 두 팀의 능력치 차이의 최소값을 구하는 과정이다.
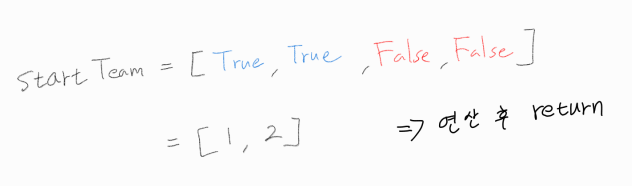




출력 예제
0
전체 코드
# 14889
def makeTeam(nowLen, nowIdx):
if nowLen == maxLen:
setAbilityGap()
return
for idx in range(nowIdx, N):
if not startTeam[idx]:
startTeam[idx] = True
makeTeam(nowLen + 1, idx)
startTeam[idx] = False
def setAbilityGap():
global abilityGap
startTeamAbility = 0
linkTeamAbility = 0
for x in range(N):
for y in range(x + 1, N):
if startTeam[x] and startTeam[y]:
startTeamAbility += (table[x][y] + table[y][x])
elif not startTeam[x] and not startTeam[y]:
linkTeamAbility += (table[x][y] + table[y][x])
abilityGap = min(abilityGap, abs(startTeamAbility - linkTeamAbility))
if __name__ == "__main__":
N = int(input())
table = []
for i in range(N):
table.append(list(map(int, input().split())))
maxLen = N // 2
people = [i for i in range(N)]
startTeam = [False for _ in range(N)]
startTeam[0] = True
# 능력치 최소값 1, 두 사람이 같은 팀을 때 최소값 2
# 능력치 최대값 100, 두 사람이 같은 팀일 때 최대값 200
# 팀 최대 인원 10명 -> 능력치 차이 최대값 200 * 10 - 2 * 10
abilityGap = 1981
makeTeam(1, 1)
print(abilityGap)
풀이 후기
백트래킹과 더불어 중복 연산을 얼마나 더 없앨 수 있는지를 묻는 문제였다고 생각한다.
'BOJ' 카테고리의 다른 글
| [Python 파이썬] 백준 3085번 - 사탕 게임 (0) | 2024.07.12 |
|---|---|
| [Python 파이썬] 백준 1182번 - 부분수열의 합 (0) | 2024.07.12 |
| [JavaScript 자바스크립트], [Python 파이썬] 백준 2606번 - 바이러스 (0) | 2024.07.08 |
| [Python 파이썬] 백준 2644번 - 촌수계산 (0) | 2024.07.08 |
| [JavaScript 자바스크립트] 백준 15662번 - 톱니바퀴(2) (0) | 2024.07.04 |


