| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 스택
- 백준 알고리즘
- 너비 우선 탐색
- 완전탐색
- javascript
- 데이터베이스
- 그래프 이론
- 너비우선탐색
- 그리디 알고리즘
- 백준알고리즘
- BFS
- oracle
- 다익스트라
- 오라클
- 브루트포스 알고리즘
- Python
- SW Expert Academy
- DP
- 브루트포스
- SWEA
- 그래프 탐색
- 문자열
- 구현
- 이분 탐색
- 프로그래머스
- 파이썬
- 다이나믹 프로그래밍
- DFS
- 백트래킹
- 자바스크립트
- Today
- Total
민규의 흔적
[알고리즘] 0-1 Knapsack Problem (0-1 냅색 문제)[SWEA 3282번 - 0/1 Knapsack] 본문
2024년 5월 16일
0-1 냅색 문제를 풀어보며 해당 이론에 대해 알아보도록 하겠다.
문제 링크 : SWEA 3282번 - 0/1 Knapsack
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
문제 접근
제목에서 친절하게 0-1 냅색 문제임을 알려주었다.
Knapsack 문제는 배낭 문제라고도 하며, 0-1 Knapsack 문제와 Fractional(분할 가능한) Knapsack 문제
가 존재한다.
둘의 차이점은 다음의 예시를 보며 설명하겠다.
민규는 고향으로 내려가기 전, 배낭에 선물을 담아 가져갈 것이다.
선물을 무한정 담으면 좋겠지만, 배낭의 한계 무게 W를 초과하면 배낭이 찢어진다.
민규는 각각의 선물의 무게와 값어치를 매겨놓았다.
고향에 내려가기 전, 배낭의 한계 무게 W를 초과하지 않는 선에서 선물을 이것 저것 넣었을 때, 가장 높은 총 값어치는 얼마인가?
만약 선물을 더 낮은 단위로 쪼갤 수 있다면 Fractional Knapsack 문제이며,
선물을 쪼갤 수 없다면 0-1 Knapsack 문제이다.
Fractional Knapsack 문제라면 단위 무게 당 이익을 기준으로 그리디 방법을 주로 사용하며,
0-1 Knapsack문제라면 위와 같은 그리디 방법이 불가능하여 DP 방식을 주로 이용한다.
위 문제는 0-1 Knapsack 문제이기에 DP 방식을 사용할 것이다.
문제에 접근하기 전, 입력 값이 다음과 같다고 가정해보자 (이는 실제 테스트케이스 입력 값과 같다.)
물건의 개수 4, 가방의 최대 부피 5
각 물건의 부피
[ 1, 3, 4, 2 ]
각 물건의 가치
[ 2, 2, 4, 3 ]
가방의 최대 부피 이하로, 4개의 물건 중 어떤 것은 넣고 어떤 것은 넣지 않음으로써 최대의 가치를 뽑아내면 된다.
여기에서 우리는 Bottom-Up에 기반한 DP 방식으로 원하는 결과에 접근할 것이다.
또한 DP 문제이므로 점화식을 찾아야 한다.
후술하겠지만, 해당 문제의 점화식은 다음과 같다.
vi = 현재 가방에 넣어보려는 물건의 부피
ci = 현재 가방에 넣어보려는 물건의 가치
i = 현재 넣어보려는 물건을 포함해 가방에 넣을 총 물건의 개수
w = 가방의 한계 부피
w = 3이라면, 가방의 한계 부피가 3일 때 라고 가정한 것.
dp[ i ][ w ] = 가방에 현재 넣을 물건을 포함 i개 넣으려 하고, 가방 한계 부피가 w라고 가정했을 때,
가방에 담을 수 있는 최대 가치
i번째 물건을 한계부피가 w인 가방에 넣으려고 할 때, 최대 가치를 구하고 싶다. (dp[i][w] 구하기)
'''
dp[i][w] 구하는 점화식
'''
if vi > w (넣으려는 물건의 부피가 가방 한계부피보다 크다면 넣지못함) :
dp[ i ][ w ] = dp[ i - 1 ][ w ] # 해당 물건을 넣기 전의 상태(가치)를 그대로 가져옴
else (넣으려는 물건이 가방에 들어갈 수 있다면 넣어보기위해 경우의 수를 따짐) :
# 해당 물건을 넣을 공간을 창출해(w - vi), 해당 물건을 넣어본 상태의 가치를 합산.
# 합산한 가치와, 해당 물건을 넣기 전의 상태(가치)를 비교하여 더 큰 값을 대입함.
dp[ i ][ w ] = max( dp[ i - 1 ][ w ], dp[ i - 1 ][ w - vi ] + ci )
Bottom - Up
1. 어떤 물건을 한계 부피가 5인 가방에 넣는 경우의 수는, 어떤 물건을 한계 부피가 0~4인 가방에 넣는 경우의 수를 포괄한다.
한계 부피가 0일 때의 물건을 넣는 경우의 수는 한계 부피가 1일 때의 물건을 넣는 경우의 수의 부분집합이고,
한계 부피가 1일 때의 물건을 넣는 경우의 수는 한계 부피가 2일 때의 물건을 넣는 경우의 수의 부분집합이고,
...
한계 부피가 4일 때의 물건을 넣는 경우의 수는 한계 부피가 5일 때의 물건을 넣는 경우의 수의 부분집합이다.
우리는 가방의 한계 부피가 0일 때부터 5일 때까지 각각의 최대 가치를 계산할 것이다.
A 물건의 부피 = 2, 가치 = 1라면 다음과 같이 나타낼 수 있다.

W = 0인 경우는 W = 1인 경우의 부분집합이다. (아무것도 넣지 않는 경우)
W = 1인 경우는 W = 2인 경우의 부분집합이다. (W = 2 :아무것도 넣지 않거나 A를 넣는 경우. W = 1 : 아무것도 넣지 않는 경우)
...
W = 4인 경우는 W = 5인 경우의 부분집합이다.
2. 가방에 어떤 물건을 넣어 이전 가치(물건을 넣지 않았을 때의 가치)와 비교해보고 싶다면, 해당 물건을 넣을 수 있는 공간이 존재하게끔 만들고 물건을 넣었을 때의 가치와 비교해보면 된다.
추가로 B 물건의 부피= 3, 가치 = 3일 때, B 물건 또한 가방에 넣을 수 있다고 가정해보자

그리고 그림과 같이 한계 부피가 4인 가방에 A, B 물건을 넣어보려고 한다. 이는 다음과 같은 부분 집합으로 나눌 수 있다.
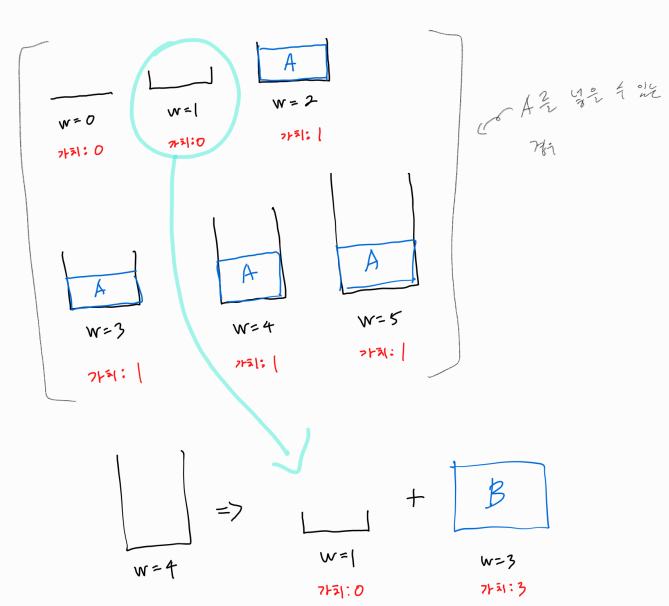
W = 4에서 3만큼 차감해준다. 이는 B 물건을 무조건 넣어보기 위함이다.
B를 넣을 부피를 만들어주고, 남은 부피는 W = 1이다.
이 부분집합은 한계 부피가 1이고 A 물건을 넣을 수 있을 때의 최대 가치를 가지고 있다.
이런 식으로 이전에 구했던 부분집합의 경우를 가져와 활용하는 것이다.
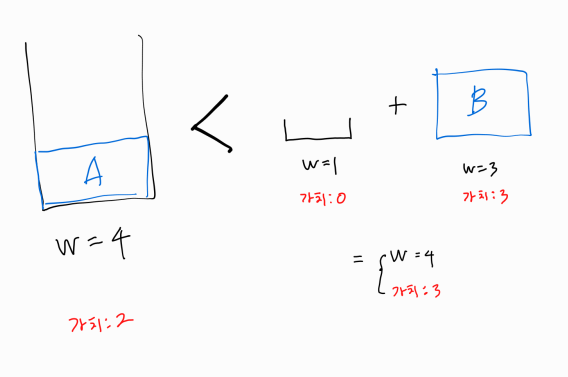
위 경우, 한계 부피가 4인 가방에 A 물건을 넣었을 때와 B 물건을 넣을 수 있을 때의 가치를 비교하여 더 큰 후자의 값이 한계부피 4일때의 최대 가치가 된다.
다시 문제로 돌아와보자.
물건의 개수 4, 가방의 최대 부피 5
각 물건의 부피
[ 1, 3, 4, 2 ]
각 물건의 가치
[ 2, 2, 4, 3 ]
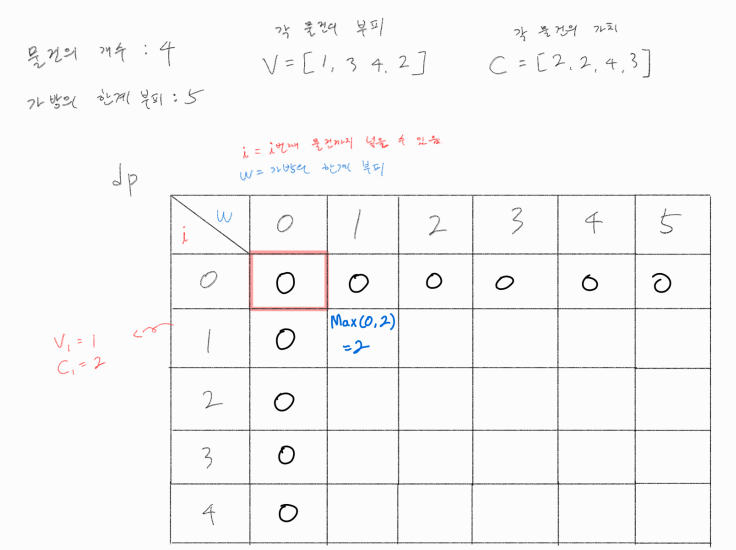
DP를 활용하여 풀기 위해 다음과 같이 2차원 배열을 선언해주자.

2차원 배열인 dp의 각 요소는 최대 가치를 의미한다.
만약 dp[2][4]의 값이 4라면, 한계 부피가 4인 가방에 2번째 물건까지 넣을 수 있을 때의 최대 가치가 4라는 것을 의미한다.
DP 초기화
위 2차원 배열에서, 0행과 0열은 모두 0으로 초기화 해준다.
0행은 가방에 아무 물건도 넣지 않겠다는 의미이므로 가치가 0이고,
0열은 가방의 한계 부피가 0이라는 의미이므로 어느 물건도 넣을 수 없기에 가치가 0이기 때문이다.

1 번째 행 채우기
이제 첫 번째 행을 채워보겠다.
첫 번째 행은 첫 번째 물건을 가방에 넣어보겠다는 의미이며, 각 열은 각각의 가방 한계 부피일 때의 최대 가치를 나타낸다.

첫 번째 물건의 부피가 1 이므로, 최소한 가방의 한계 부피가 1이어야 첫 번째 물건을 넣어볼 수 있다.
가방의 한계 부피가 1일 때 첫 번째 물건을 무조건 넣어본 후 가치를 알아내기 위해선, 가방에 적어도 A가 들어갈 부피는 마련되어 있어야 한다. 해당 경우는 가방의 한계 부피가 0이고 아무 물건도 넣지 않은 가방의 최대 가치 + 첫 번째 물건의 가치로알 수 있다.
위 그림에서, 가방의 한계 부피가 0이고 아무 물건도 넣지 않은 가방의 최대 가치를 나타내는 위치는 빨간색 영역 표시한 부분이다.
이를, 첫번째 물건을 절대 넣지 않고 한계 부피가 1인 가방의 최대값과 비교하여, 더 큰 가치를 해당 dp 요소에 대입해주면 된다.
첫 번째 물건을 절대 넣지 않고 한계 부피가 1인 가방의 최대 가치는 0이고, 가방의 한계 부피가 1일 때 첫 번째 물건을 무조건 넣어보는 경우의 가치는 2이므로, 더 큰 가치인 2를 dp 요소에 대입한다.
이와 같은 방식으로 나머지 열도 채워준다.

dp[1][5] = 2 이므로, 가방의 한계 부피가 5일 때 첫 번째 물건을 넣을 수 있다면 최대 가치는 2라는 의미이다.

2 번째 행 채우기
두 번째 물건까지 넣을 수 있을 때의 최대 가치를 각각 계산해보자.

두 번째 물건의 부피가 3이므로 가방의 한계 부피가 최소 3이어야 한다. 그 미만의 한계 부피일 때에는 절대 넣을 수 없으므로 첫 번째 물건까지 넣었을 때의 최대 가치를 그대로 가져온다.

가방의 한계 부피가 3이라면 두 번째 물건을 넣어볼 수 있다.
해당 dp 위치의 요소는 다음 두 가치 중 더 큰 가치를 대입하면 된다.
두 번째 물건을 넣지 않을 때의 최대 가치 vs 두 번째 물건을 무조건 넣을 때의 가치
두 번째 물건을 넣지 않을 때의 최대 가치는 같은 열 바로 윗 행의 가치와 같으며,
두 번째 물건을 무조건 넣을 때의 가치는 해당 물건이 들어갈 부피가 확보되었을 때의 가치(표의 빨간색 영역) + 두 번째 물건의 가치이다.
한계 부피가 3이므로, 한계 부피가 0인 가방에 첫 번째 물건까지 넣었을 때의 최대 가치 + 두 번째 물건의 가치이다.
계산 결과 두 가치는 같으므로 둘 중 아무 가치나 삽입한다.

dp[2][4]의 값은,
두 번째 물건을 넣지 않았을 때의 최대 가치와, 두 번째 물건을 무조건 넣었을 때의 가치 중 큰 가치를 대입하면 된다.
두 번째 물건을 넣지 않았을 때의 최대 가치 = dp[1][4] = 2
두 번째 물건을 무조건 넣었을 때의 가치 = dp[1][4 - 3] + 2 = 4
여기서 점화식을 찾을 수 있다.
vi : 현재 넣어보려는 물건의 부피
ci : 현재 넣어보려는 물건의 가치
i : 현재까지 i개의 물건을 넣어볼 수 있었다는 뜻이며, 지금 i번째 물건을 가방에 넣어볼 수 있다는 뜻
w : 현재 가방의 한계 부피
위와 같을 때,
if w < vi: # 현재 넣어보려는 물건을 넣을 수 없음
dp[ i ][ w ] = dp[ i - 1 ][ w ]
else: # 현재 넣어보려는 물건을 넣고 안넣고의 가치를 비교해봄
dp[ i ][ w ] = max(dp[ i - 1 ][ w ], dp[ i - 1 ][ w - vi ] + ci )
위 점화식으로 나머지 dp 요소들을 채워보자.

3 번째 행 채우기

3 번째 물건을 넣을 수 있을 때의 최대 가치 또한, 위에서 사용한 방법을 그대로 활용하며 알아내면 된다.

가방의 한계 부피가 3 번째 물건의 부피보다 작으므로 절대 넣을 수 없어, 각각 같은 열 윗 행의 값을 대입한다.
dp[3][1] = dp[2][1]
dp[3][2] = dp[2][2]
dp[3][3] = dp[2][3]

가방에 3번째 물건을 넣을 부피가 된다면,
3번째 물건을 무조건 넣는 경우의 가치와 3번째 물건을 절대 넣지 않는 경우의 가치를 비교해본 후 더 큰 가치를 삽입한다.

4 번째 행 채우기


현재 넣을 수 있는 물건의 부피보다 가방의 한계 부피가 더 작다면 같은 열 윗 행의 가치를 그대로 대입한다.

물건을 넣을 수 있다면 위의 방식대로 더 큰 가치를 찾아 대입하면 된다.



로직 종료

우리가 알고 싶은 값은, 물건 4개를 한계 부피 5인 가방에 넣었을 때 최대 가치를 구하는 것이다.
해당 결과 값을 가지고 있는 dp 값인 dp[4][5]를 출력해주면 된다.
순서도
1. 물건의 개수 N, 가방의 한계 부피 K를 입력받고, 각 물건의 부피와 가치를 v, c 배열에 append한다.
2. DP를 활용하여 최대 가치를 산정해 나간다. 그러기 위해 2차원 배열 dp를 선언한다.
3.dp를 하나씩 채워나간다.
3-1. 가방의 한계 부피보다 현재 물건의 부피가 더 크면 해당 물건을 넣지 않는 가치로 갱신한다.
3-2. 현재 물건을 가방에 넣을 수 있다면,
해당 물건을 가방에 무조건 넣었을 때의 가치와 해당 물건을 가방에 무조건 넣지 않을 때의 최대 가치 중
더 큰 가치로 갱신한다.
4. dp의 마지막 행 마지막 열 값을 출력한다.
입력 예제
1
4 5
1 2
3 2
4 4
2 3
출력 예제
#1 6
주의할 점
각 물건은 하나 씩만 존재함에 유의한다. 첫 번째 물건을 2개 이상 넣는 경우는 존재하지 않는다는 의미이다.
전체 코드
def solution():
for row in range(1, N + 1):
for col in range(1, K + 1):
# 가방 한계 부피보다 현재 물건의 부피가 크면 어떤 경우든 넣지 못함
if col < v[row]:
dp[row][col] = dp[row - 1][col]
else:
dp[row][col] = max(dp[row - 1][col], dp[row - 1][col - v[row]] + c[row])
return dp[N][K]
T = int(input())
for t in range(1, T+1):
N, K = map(int, input().split())
dp = [[0 for _ in range(K + 1)] for _ in range(N + 1)]
# 0번째 인덱스는 더미값
v = [0]
c = [0]
for _ in range(N):
_v, _c = map(int, input().split())
v.append(_v)
c.append(_c)
print(f'#{t} {solution()}')
풀이 후기
DP를 활용하는 문제이므로 DP에 익숙하지 않다면 DP 문제를 많이 풀어봐야 한다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 패턴 매칭 알고리즘, KMP 알고리즘 ( Knuth–Morris–Pratt Algorithm ) (6) | 2024.10.10 |
|---|---|
| [알고리즘] 다익스트라(Dijkstra) [ 백준 1916번 - 최소비용 구하기 ] (0) | 2024.05.22 |
| [알고리즘] LIS(최장 증가 부분 수열), 응용 문제 3가지 (0) | 2024.04.16 |
| [알고리즘] 플로이드-워셜(Floyd-Warshall) 알고리즘 [백준 11404번 - 플로이드] (2) | 2023.10.27 |
| [알고리즘] 깊이우선탐색(DFS), 너비우선탐색(BFS) [ 백준 1260번 - DFS와 BFS ] (0) | 2023.09.20 |




